Az eredeti oldal a következő címen érhető el:
http://www.grad.hr/geomteh3d/prodori/prodor_stst.html
This post is the translation of the website supported by the project 3DGeomTeh.(The original site is avaible in Croatian.)
The original site is available here:
http://www.grad.hr/geomteh3d/prodori/prodor_stst.html
Kúpok áthatása
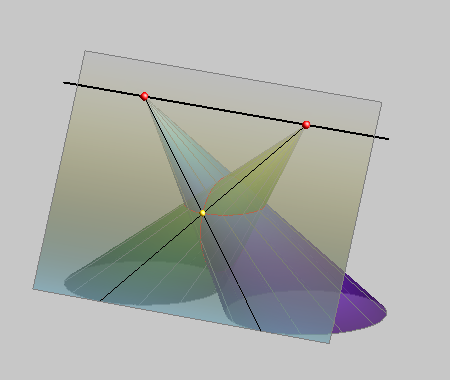
A kúpok áthatásának nehézsége, hogy az áthatásban résztvevő kúpokból egyszerre csak akkor tudunk könnyen szerkeszthető metszetet készíteni, ha a segédsík a kúpok csúcspontján áthalad, azaz tartalmazza a csúcspontokat összekötő egyenest.
A fenti ábrán ezt a síkot meglengetjük, ezzel minden pillanatban négy újabb közös pontot nyerünk.
Az ábra kúpjai speciálisan vannak elhelyezve, ugyanis érintkeznek. Így ha a lengő segédsíkot éppen a közös érintősíknak választjuk, akkor csak egyetlen közös pontot kapunk: annak a két alkotónak a metszéspontját, melyekben a sík a kúpokat érintette:
Az áthatási görbe állhat egyetlen ágból, vagy két ágból vagy egyetlen ívből, melynek kettőspontja van:Az ábra kúpjai speciálisan vannak elhelyezve, ugyanis érintkeznek. Így ha a lengő segédsíkot éppen a közös érintősíknak választjuk, akkor csak egyetlen közös pontot kapunk: annak a két alkotónak a metszéspontját, melyekben a sík a kúpokat érintette:
|
|
|
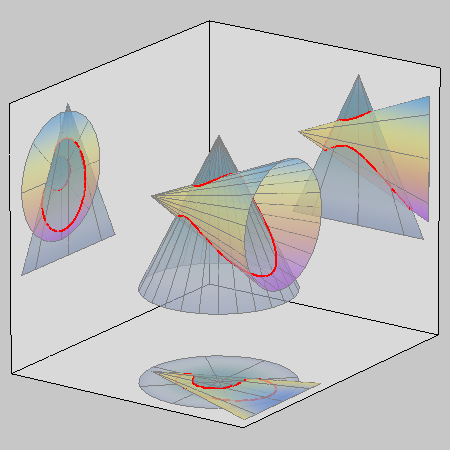
| A keletkező egyetlen ág mindkét kúpot csak részben öleli át. | A keletkező két ív az egyik kúppaláston csak lyukakat üt. A másik paláston teljesen körbefut, ezzel azt három elkülönülő részre bontja. |
|
|
|
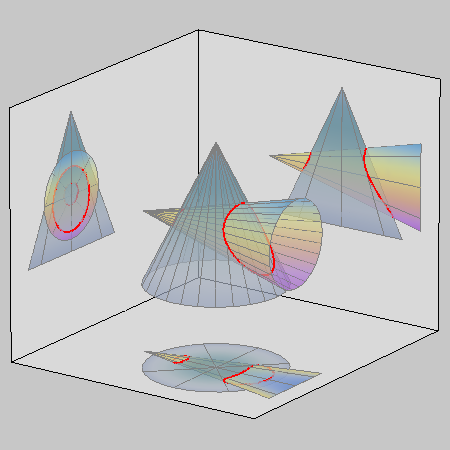
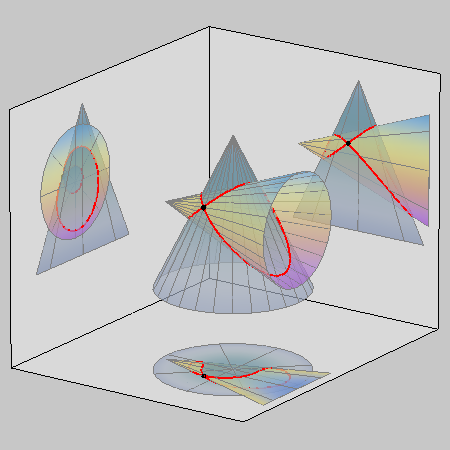
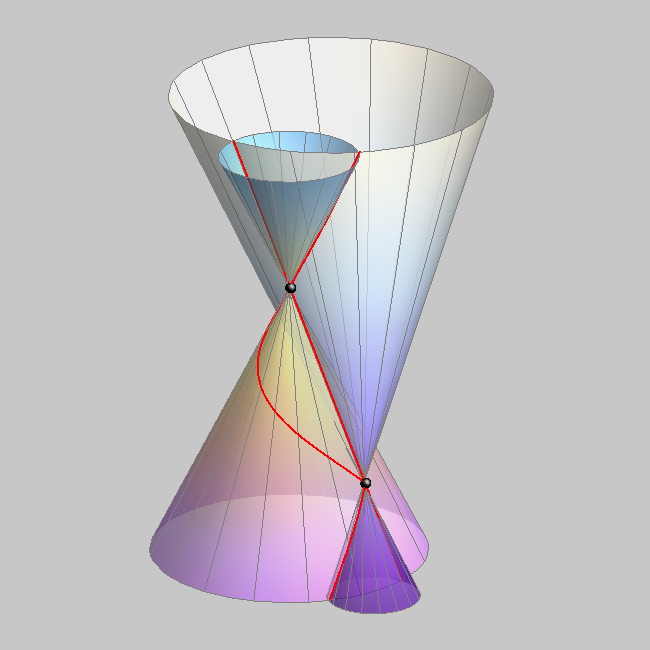
| Érintkező kúpok esetén az áthatási görbének kettőspontja lesz, és a 8-as forma csak az egyik paláston fut körbe. | Kettősponttal rendelkezik a görbe akkor is, ha az egyik kúp csúcspontja a másik palástjára illeszkedik, de ott nem érintkeznek a felületek |
Széteső áthatás
Széteső áthatásról akkor beszélünk, ha az áthatásként adódó negyedrendű görbe felbomlik alacsonyabb rendű görbék együttesére.
|
|
|
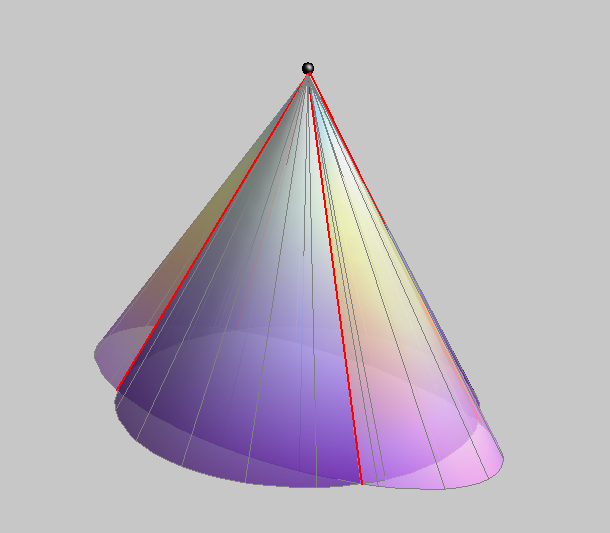
| Ha a kúpok két pontban is érintkeznek, akkor a keletkező áthatásnak két kettőspontja lesz és két kúpszeletre esik szét. Az ábrán két, különböző síkban fekvő ellipszist kaptunk. | Ha az egyik kúp vezérgörbéje ellipszis, és kúpok közös csúcsponttal rendelkeznek, akkor az áthatási görbe a négy közös alkotó együttese lesz. |
|
| |
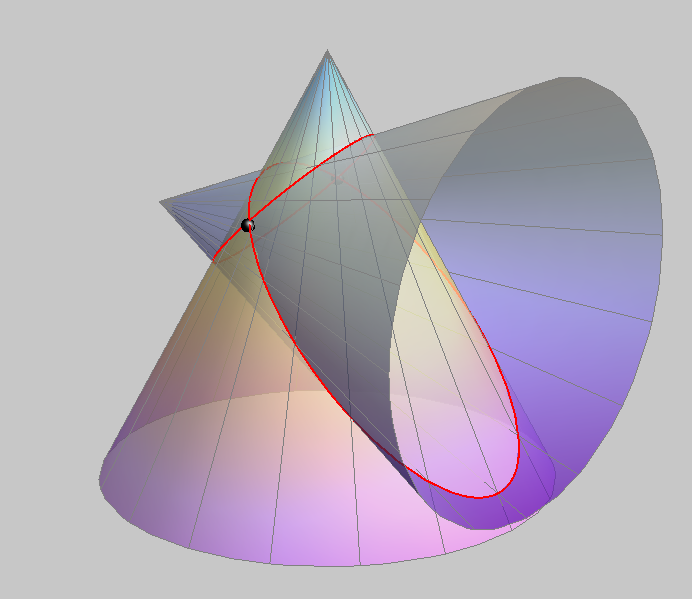
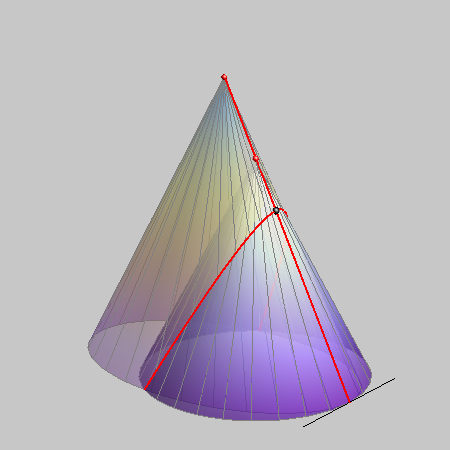
| Ha a két kúp egy alkotó mentén érintkezik, akkor ezt az alkotót duplán számítjuk az áthatásban, és a "maradék" görbe egy kúpszelet lesz. Az ábrán látható felvételben ez egy parabola. | Ha a két kúpnak van közös alkotója, de ebben nem érintkeznek, akkor ehhez az alkotóhoz még egy harmadrendű térgörbe társul az áthatás részeként. |


Nincsenek megjegyzések:
Megjegyzés küldése