Kezdődik a nyári szünet!

Mindenkinek kellemes nyarat kívánok!

Fedélidomok szerkesztése

A fedélidomszerkesztés egy gyakorlatias témakör a síkok metszése és poliéderek áthatása alkalmazására. A feladatunk az lesz, hogy az épületek lefedésekor használatos tetősíkokat kialakítsuk.

Adottak az egy magasságban lévő ereszvonalak.
Feltételezzük, hogy az ereszvonalakra egyenlő hajlásszögű tetősíkokat illesztünk. A nálunk szokásos síkállás az amelyben a síkok a vízszintes síkkal 45 fokos szöget zárnak be. Mivel egyetlen gyakorlat erejéig foglalkozunk a témakörrel így csak az alapokkal foglalkozunk. A feladatok egyetlen vetületen megoldhatók, csak a felülnézetet fogjuk használni.
Ha a tető keresztmetszetét nézzük, akkor az előbb említett 45°-os szögnek annyi hatása van, párhuzamos ereszvonalak esetén a tetősíkok összemetsződéseként kapott gerinc fele akkora magasan lesz az ereszvonal fölött, mint amekkora az ereszvonalak távolsága volt.

Még egy fontos dolgot is észrevehetünk: felülről nézve a gerinc éppen félúton lesz az ereszvonalak között. Geometria nyelvén: középpárhuzamost látunk. A fenti ábrán az is látszik, hogy ha eltérnék a 45%-os hajlásszögtől, akkor csak a tető (gerinc) magasságán változtatnánk, de a gerinc vetülete továbbra is középpárhuzamosként látszana. De vajon mi a helyzet az egymáshoz valamilyen szögben csatlakozó ereszvonalak esetén. Mit látunk a a tetősíkok metszésvonalából az élgerinc és a vápa esetén? Erre mutatok egy példát, amikor az egyik feladatunk modelljét egy 3D nyomtató szeletelőprogramjában megnyitottam, és felszeleteltem:

Felülről nézve a tetősíkokat kirajzoló vonalak úgy látszanak, mintha az ereszvonalat belülről egy vastag filctollal újra és újra körberajzoltuk volna. A modellezésben az ilyen típusú vonalakat offset vonalaknak hívják. De miután az eresz vonaltól mindig ugyanolyan távolságra haladnak, a csúcsokban az irányváltások miatt mindig kirajzolják az élgerincek és vápák vonalát, melyek iránya mindig szögfelező állású lesz.

 

 

Letölthető anyagok

• Diasor   
• Munkafüzet2025, 40-44. o.
• Fedélidom szerkesztés (segédlet)

További segédanyag

• Fedélidomok_hallgatói munkák
• Néhány feladat megoldása+1 lap 
• Gyakorló feladatok - fedélidom  
• Fedélidomok

Boltozatok szerkesztése

Az utolsó témánk a boltozatszerkesztés, melyben hengereket és gömböket használunk különböző terek lefedésére.  A legegyszerűbb a téglalap alakú terület lefedésére használatos dongaboltozat, illetve a kör alakú terület lefedésére használatos gömbkupola. Először a félgömb vágásával nyerjük a cseh- és a csehsüvegboltozatot, majd a félhengerek áthatásával a kereszt- és kolostorboltozatot. De ezek csak az alapot adják az összetett boltozatok kialakításához.Szabálytalan terek lefedésével és különböző szélességű folyosókat lefedő dongaboltozatok összemetsződésével találkozhatunk.

A félgömbből síkmetszéssel nyert boltozatok:

Cseh boltozat	Cseh süvegboltozat	Csegelyes kupola

Hengerből áthatással nyert boltozatok:

Keresztboltozat	Kolostorboltozat

Szükségesek:

• Diasor
  
• Munkafüzet2025, 66. oldalától a végéig

Szemléltető videók:

További segédanyag: 

• Hallgatói munkák
• A GeomTech3D projekt keretében készült segédanyag (a szöveg horvát nyelvű, de az ábrák szemléletesek.) 
• A dongaboltozatok áthatásával keletkező boltozat szerkesztésének lépései táblaképek alapján
• Hasznos lista a forgásfelületek témakörhöz
• Boltozat szemléltetése naranccsal 

Forgásfelületek áthatása

Letölthető anyagok:

• Diasor 11 és Diasor 12
• A vetített diasorban szereplő animált ábra: kúp és henger áthatása
  
• Munkafüzet2025 56-65. oldalai

Ez a témakör a korábbi síklapú testek áthatása témakör továbbgondolása, ugyanis legvégül minden forgásfelület (de a szépen hullámzó ún. szabad formájú felületek is) poliéderekkel vannak közelítve a megjelenítések vagy az előállítások során. Ahhoz, hogy kezelhetők legyenek, bizonyos metszeteket kell ismernünk.
Az áthatásszerkesztés módszerei és ötletei attól függhetnek, hogy a felületek tengelyei egymáshoz képest hogyan helyezkednek el.

1. Egybeeső tengelyek

esetén a felületek  paralel körökben metszik egymást. A meridiángörbék közös pontjait kell keresni, ezek forgatásával nyerjük az áthatást adó kört (köröket).(Lásd Mf. 56. oldala)

2. Párhuzamos tengelyek 

esetén megadott felületeket a tengelyükre merőlegesen szeleteljük. Egy ilyen szeletelősíkban mindkét felület egy-egy (ritkán több) paralel köre rajzolódik ki. Ezek közös pontjai az áthatási görbe pontjai lesznek. Célszerű elég sűrűn szeletelni, hogy a kapott pontok minél jobban megmutassák az áthatási görbe formáját. (Lásd 57-61. oldalak)
Az áthatási görbének vannak szélső helyzetű (legmagasabban, legalacsonyabban lévő), kontúron lévő és a felületek közös szimmetriasíkjában lévő pontjai, ezeket jól választott szeletelősíkokkal tudjuk meghatározni. Ilyen helyzetet szemléltet az alábbi videó, amely 59. oldal feladatának a modelljén mutatja be a szeletelő eljárást.

A 60. oldal feladatának különlegessége, hogy a gömb érinti a kúpot. Ez azért érdekes helyzet, mert ebben a pontban kialakul egy ún. kettőspont. A görbén végighaladva ezen a ponton irányváltás nélkül jutunk át. A görbe futásának érzékeléséhez érdemes a 61. oldalon az áthatási vonalon 10-15 pontot beazonosítani és azokat az eredeti felületekkel együtt transzformálni.
A bal oldali ábra a modellt, a jobb oldalin a felületek kikapcsolva, csak a kontúrok, perem, és az áthatási görbe látszik:

3. Metsző helyzetű tengelyek

esetében olyan példákat fogunk látni, ahol a tengelyek merőlegesek egymásra. Miért jó ez? Ez egy igen fontos könnyítés egy álló forgásfelület és egy fekvő helyzetű henger esetén, mert így hengert vízszintes síkokkal könnyen tudjuk alkotókban metszeni.
A módszerünk:

SZELETELÉS !!!

Már nem azon kell gondolkodnunk, hogy mi a szeletelés, hanem alkalmazni azt SOKSZOR. Ezzel lehet biztosítani, hogy nagyon közel lesznek megszerkesztett pontok, amiket össze kell kötni. De látatlanban nem lehet megtanulni azt, hogy milyen is lesz egy áthatási vonal futása, ezért lássunk néhány példát:

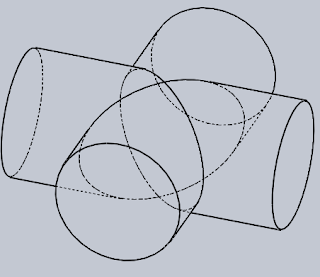
Ez a két henger egyenlő sugarú és a tengelyeik metsző helyzetben vannak. Alapban bárhogy elhelyezkedhetnek a térben, ezeken a képeken "fekvő" helyzetben vannak. Vagyis így, ahogy vannak, le lehet tenni őket az asztalra és egy lappal le lehet fedni őket. A geometria nyelvén ez azt jelenti, hogy alulról és felülről ugyanaz a síkpár érinti mindkét hengert → a legalsó és a legfelső alkotók metszéspontjaiban  a hengerek érintik egymást, és az áthatási vonal szétesik két ellipszisre. Ezek vonala a fenti képeken nagyon szépen kirajzolódik. Az ellipszisek síkjai egymásra merőlegesek, felülről nézve X-et formáznak. Ezzel a helyezettel még fogunk találkozni a Boltozatok témánál.

Ha az előbbi helyzeten csak annyit változtatunk, hogy csökkentjük a sugarát, akkor a fentebb említett érintkezést alul is és felül is elrontjuk. Egyszerűen a sárga henger vastagabb, a szürke vékonyabb és csak amiatt marad meg a levegőben, mert átdugtuk a sárga hengeren.

Ilyenkor az áthatásvonala két különálló zárt vonalból áll. Ezek szimmetrikusan helyezkednek el és kb olyasmi tekeredésük van, mint a Pringles csipsz peremének.

A PEREMet kell figyelni, és nem a csipsz felületét! A lényeg, hajlása van felfelé és lefelé is.

Hogyan érdemes szeletelni?

Az előbbi esetekben a forgástengelyek síkja mindkét felületnek szimmetriasíkja. Egy ilyen szeletelő síkban a hengerekből egy-egy alkotópárt találunk, melyek összesen 4 metszéspontot határoznak meg.

Vagyis a teendő: minél többször felvenni ilyen szeletelő síkot és négyesével megszerkeszteni a pontokat. Gyors és egyszerű eljárás! A munkafüzet 62. oldalán a vastagabb henger álló helyzetben van és a vékonyabb vízszintesen fúrja át. Ez azt jelenti, hogy ott a szeletelősíkjaink függőleges helyzetűek leszek, egészen pontosan a K2-vel párhuzamosak.

Az előbbi hengereket szeletelhetjük az egyik tengelyre merőlegesen is. Ekkor az egyik hengerből paralel kört, a másikból alkotópárt metszünk. Az egy szeletelősíkban lévő metszetek közös pontjai kijelölhetők. Valahogy így: 

Ez is gyors módszer, mint ahogy a képen is látszik, egy lépésben 4 pontot tudunk előállítani.

4. Kitérő helyzetű tengelyek

Ha a tengelyeket a metsző helyzetből elmozdítjuk, akkor kitérő tengelyeket kapunk. Kitérő tengelyek esetén általában az egyik tengelyre merőlegesen érdemes szeletelni. Ebben a szemléltető példában egy fekvő henger és függőleges tengelyű kúp került áthatásra. A szerkesztést megkönnyíti, ha a hengert vetítő helyzetűvé transzformáljuk. És ebben a helyzetben a szeletelést vízszintes síkokkal érdemes elvégezni, mert akkor a kúpból kimetszett kört két hengeralkotóval kell összemetszeni.

A 65. oldal feladatában a henger a K2 képsíkra merőleges, így nem kell transzformálni.

További segédanyag:

• Részlet Pethes Endre: 222 ábrázoló geometria feladat c. könyvéből. (XI. fejezet)
• gyakorló feladatok
• Illetve a jobb oldalon ajánlott irodalomból az Ábrázoló geometria szemléletesen című könyv megfelelő fejezete
• hallgatói munkák
• Hasznos lista a forgásfelületek témakörhöz
• A blog vendégposztjai közül:  Hengerek áthatása és Kúpok és hengerek áthatása

Gömb és tórusz metszése síkkal

 Letölthető anyagok:

• Diasor a gömb metszéséről + Diasor a tórusz metszéséről
• Munkafüzet2025 51. és 55. oldalai

Emlékeztető a gömb metszetei kapcsán:

• A gömb minden metszete kör, melyet a vetületeken körnek, ellipszisnek vagy átmérő hosszúságú szakasznak látunk. 
• A gömb metszetei egyre kisebbek, ahogy a középponttól távolodunk (Lásd itt). Ezt jól lehet szemléltetni azokkal a papírmodellekkel, melyek megfelelő sugarú körlapokból építhetők.
• Ha függőleges síkokkal felszeletelünk egy gömböt, akkor a metszetek nem csúszkálnak el, le, hanem egy adott magasságban maradnak.

 Gömb metszete általános helyzetben:

A legegyszerűbb olyan vetülettel (is) dolgozni, ahol a metsző sík vetítősík, vagyis egyetlen vonal jeleníti meg. Minden metszet esetén keressük a

• legmagasabban / legalacsonyabban fekvő pontokat (ha léteznek)
• a kontúrokon lévő pontokat
• a metszet (vagy a vetületének) nevezetes pontjait
• és annyi általános helyzetű pontot, hogy a metszet íve könnyen rajzolható legyen.

Egy kis kiegészítés ahhoz, hogy hogyan képzeljük el a gömb kontúrján lévő pontokat. A kontúr vonala mindig egy adott képsíkhoz (és így egy vetülethez) tartozik. A lenti forgatható ábrán a gömbön megjelenítettem a K2 képsíkkal párhuzamos főkört, melyet a képsíkra vetítve a gömb kontúrját kapjuk. Jól látszik, hogy ez a gömbi kör és metsző sík keresztezi egymást, mert a keletkező síkmetszet nem csak az elől lévő félgömbön keletkezik, hanem átnyúlik a hátsó félgömbre is. (Ezek a pontok narancsszínű megjelenítést kaptak a diasorban.)

 Tórusz metszetei :

A tórusz metszetei negyedrendű görbék, amely azt jelenti, hogy előfordulhat, hogy egy egyenesnek a metszettel 4 közös pontja van. Ahogy azt már korábban láttuk, a forgástengelyre merőleges metszésekkel a legtöbb esetben koncentrikus köröket kapunk, kivéve, amikor a tóruszt alulról vagy felülről érinti a sík. Ez az érintkezés azért "trükkös", mert matematikailag a legfelső kör ilyenkor duplán számítható ki, vagyis két koncentrikus kör, melyeknek egyenlő a sugara. Ugyanez érvényes az alsó körre is.  (http://fluid.itcmp.pwr.wroc.pl/~eichler/torus-przek2/img/tor-prze2.gif)

Ha a forgástengellyel párhuzamosan szeletelünk, akkor sokkal változatosabb metszeteket kapunk:  "ovális", "piskóta", nyolcas, "két szembefordított tojás" vagy két kör is lehet. A 8-as forma akkor jön létre, amikor a gyűrű belsejét megérinti a sík.

Ezeket a forgástengellyel párhuzamos metszeteket is használhatjuk sliceform modellek készítésére. (lásd lentebb)

Érdekesség, hogy tóruszból nemcsak a forgástengelyre merőleges  metszéssel kaphatunk kör metszeteket. Az alábbi ábra körei az ún.  Villarceau-körök, melyeket Yvon Villarceau (1813-1883) francia csillagászról és matematikusról neveztek el. A múlt század elején igazolták, hogy ezek a körök ugyanakkora szögben metszik a a tórusz összes paralel körét. A metsző síknak két helyen érintenie kell a tórusz belső oldalát, a jobb oldali ábra vetítősíkként mutatja ezt a helyzetet.

A képek forrása:

• http://fluid.itcmp.pwr.wroc.pl/~eichler/torus-przek2/img/torus-przek-2.gif
• http://upload.wikimedia.org/wikipedia/commons/f/f1/Villarceau_circles.gif
• http://momath.org/wp-content/uploads/bagel-circles-3.jpg

További segédanyag:

•  Gömbmetszetek sora (órán szerepelt)
  
• Táblaképek egy szerkesztésről (2016): Tórusz metszése síkkal
• Hallgatói munkák (több szkennelt ábra, tórusz metszése különböző állású síkokkal)
• Hasznos lista a forgásfelületek témakörhöz
• Gömb-modell készítése: https://papercraftetc.blogspot.com/2015/03/super-pi-day-ball.html
• Tórusz-modell készítése: https://papercraftetc.blogspot.com/2013/07/sliceforms-are-my-new-obsession.html