Ezen a gyakorlaton a
forgásfelületek áthatásának szerkesztésével foglalkozunk olyan esetekben, amikor a két felület forgástengelye metsző vagy kitérő helyzetben van egymáshoz képest. A módszerek és
ötletek is alkalmazkodnak ezekhez a helyzetekhez, bár az is igaz, teljesen általános helyzetekkel nem fogunk találkozni.
Pl. A forgástengelyek egymásra merőleges helyzetben lesznek. Ez egy igen fontos könnyítés, mert így egy fekvő helyzetben lévő henger vízszintes síkokkal is könnyen szerkeszthető metszeteket ad.
A módszerünk:
SZELETELÉS !!!
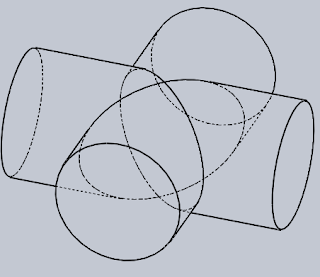
A kurzus végén már nem azon kell gondolkodni, hogy mi a szeletelés, hanem alkalmazni azt SOKSZOR. Ezzel lehet biztosítani, hogy nagyon közel lesznek megszerkesztett pontok, amiket össze lehet/kell kötni. De látatlanban nem lehet megtanulni azt, hogy milyen is lesz egy áthatási vonal futása, ezért lássunk néhány példát:
Ez a két henger egyenlő sugarú és a tengelyeik metsző helyzetben vannak. Alapban bárhogy elhelyezkedhetnek a térben, ezeken a képeken "fekvő" helyzetben vannak. Vagyis így, ahogy vannak, le lehet tenni őket az asztalra és egy lappal le lehet fedni őket. A geometria nyelvén ez azt jelenti, hogy alulról és felülről ugyanaz a síkpár érinti mindkét hengert → a legalsó és a legfelső alkotók metszéspontjaiban a hengerek érintik egymást, és az árhatási vonal szétesik két ellipszisre. Ezek vonala a fenti képeken nagyon szépen kirajzolódik. Az ellipszisek síkjai egymásra merőlegesek, felülről nézve X-et formáznak. Ezzel a helyezettel még fogunk találkozni a Boltozatok témánál.
Ha az előbbi helyzeten csak annyit változtatunk, hogy csökkentjük a sugarát, akkor a fentebb említett érintkezést alul is és felül is elrontjuk. Egyszerűen a sárga henger vastagabb, a szürke vékonyabb és csak amiatt marad meg a levegőben, mert átdugtuk a sárga hengeren.
Ilyenkor az áthatásvonala két különálló zárt vonalból áll. Ezek
szimmetrikusan helyezkednek el és kb olyasmi tekeredésük van, mint a
Pringles csipsz peremének.
A peremet kell figyelni, és nem a csipsz felületét! A lényeg, hajlása van felfelé és lefelé is. Hogyan érdemes szeletelni?
Az előbbi esetekben a forgástengelyek síkja mindkét felületnek szimmetriasíkja. Egy ilyen szeletelő síkban a hengerekből egy-egy alkotópárt találunk, melyek összesen 4 metszéspontot határoznak meg.
Vagyis a teendő: minél többször felvenni ilyen szeletelő síkot és négyesével megszerkeszteni a pontokat. Gyors és egyszerű eljárás! A munkafüzet 69. oldalán a vastagabb henger álló helyzetben van és a vékonyabb vízszintesen fúrja át. Ez azt jelenti, hogy ott a szeletelősíkjaink függőleges helyzetűek leszek, egészen pontosan a K2-velpárhuzamosak.
Az előbbi hengereket szeletelhetjük az egyik tengelyre merőlegesen is.
Ekkor az egyik hengerből paralel kört, a másikból alkotópárt metszünk.
Az egy szeletelősíkban lévő metszetek közös pontjai kijelölhetők. Valahogy így:
Ez is gyors módszer, mint ahogy a képen is látszik, egy lépésben 4 pontot tudunk előállítani.
Ha a tengelyeket a metsző helyzetből elmozdítjuk, akkor kitérő tengelyeket kapunk.
Kitérő tengelyek
esetén általában az egyik tengelyre merőlegesen érdemes szeletelni. Ebben a szemléltető példában egy
fekvő henger és függőleges tengelyű kúp került áthatásra. A szerkesztést megkönnyíti, ha a hengert vetítő helyzetűvé transzformáljuk. És ebben a helyzetben a szeletelést vízszintes síkokkal érdemes elvégezni, mert akkor a kúpból kimetszett kört két hengeralkotóval kell összemetszeni.
A 72. oldal feladatában a henger a K2 képsíkra merőleges, így nem kell transzformálni.
Ebben a témakörben 2 gyakorlat erejéig forgásfelületek áthatásával foglalkozunk. Ez a témakör a korábbi síklapú testek áthatása témakör továbbgondolása, ugyanis legvégül minden forgásfelület (de a szépen hullámzó ún. szabad formájú felületek is) poliéderekkel vannak közelítve a megjelenítések vagy az előállítások során. Ahhoz, hogy kezelhetők legyenek, bizonyos metszeteket kell ismernünk.
Az áthatásszerkesztés módszerei és
ötletei attól függhetnek, hogy a felületek tengelyei egymáshoz képest
hogyan helyezkednek el. Ezen a gyakorlaton az egybeeső és a párhuzamos tengelyű forgásfelületekkel foglalkozunk
Egybeeső tengelyek
esetén a felületek paralel körökben metszik egymást. A meridiángörbék
közös pontjait kell keresni, ezek forgatásával nyerjük az áthatást adó
kört (köröket).
Párhuzamos tengelyek
esetén megadott felületeket a tengelyükre merőlegesen szeleteljük. Egy
ilyen szeletelősíkban mindkét felület egy-egy (ritkán több) paralel köre
rajzolódik ki. Ezek közös pontjai az áthatási görbe pontjai lesznek.
Célszerű elég sűrűn szeletelni, hogy a kapott pontok minél jobban
megmutassák az áthatási görbe formáját.
Az
áthatási görbének vannak szélső helyzetű (legmagasabban,
legalacsonyabban lévő), kontúron lévő és a felületek közös
szimmetriasíkjában lévő pontjai, ezeket jól választott szeletelősíkokkal
tudjuk meghatározni. Ilyen helyzetet szemléltet az alábbi videó, amely 66. oldal feladatának a modelljén mutatja be a szeletelő eljárást.
A 67. oldal: feladatának különlegessége, hogy a gömb érinti a kúpot. Ez azért érdekes helyzet, mert ebben a pontban kialakul egy ún. kettőspont. A görbén végighaladva ezen a ponton irányváltás nélkül jutunk át. Az alábbi képek ezt a helyzetet szemléltetik többféle nézőpontól. (További képek a feladat modelljéről)
A modell
A felületek kikapcsolva, csak a kontúrok,
perem, és az áthatási görbe látszik.
Alulról beleláthatunk a modell belsejébe
(üreges modell)
A szeletelés egy lépése: mindkét testből paralel kört metszünk, ezek közös pontjai az áthatási görbe két pontját adják.
Gömb metszete:
A gömb minden metszete kör, melyet a vetületeken körnek, ellipszisnek vagy átmérő hosszúságú szakasznak látunk.
A gömb metszetei egyre kisebbek, ahogy a középponttól távolodunk. Ezt jól lehet szemléltetni azokkal a papírmodellekkel, melyek megfelelő sugarú körlapokból építhetők.
További képek elérhetők itt: https://www.thingiverse.com/thing:3514453
Ha papírból készült modellünk van, akkor az teljesen jól összehajtató, ahogy a lenti képen is látható.
Egy kis kiegészítés ahhoz, hogy hogyan képzeljük el a gömb kontúrján lévő pontokat. A gömbön megjelenítettem a K2 képsíkkal párhuzamos főkört, melyet a képsíkra vetítve a gömb kontúrját kapjuk. Jól látszik, hogy ez a gömbi kör most átmetszi a metsző síkot. Ezek a pontok narancsszínű megjelenítést kaptak a diasorban.
Tórusz metszete:
A tórusz metszetei negyedrendű görbék, amely azt jelenti, hogy előfordulhat, hogy egy egyenesnek a metszettel 4 közös pontja van. Az alábbi animált ábra a forgástengelyre merőleges metszeteket mutatja. A legtöbb esetben koncentrikus köröket kapunk, kivéve, amikor a tóruszt alulról vagy felülről érinti a sík. Ez az érintkezés azért "trükkös", mert matematikailag a legfelső kör ilyenkor duplán számítható ki, vagyis két koncentrikus kör, melyeknek egyenlő a sugara. Ugyanez érvényes az alsó körre is.
Ha a forgástengellyel párhuzamosan szeletelünk, akkor sokkal változatosabb metszeteket kapunk: "ovális", "piskóta", nyolcas, "két szembefordított tojás" vagy két kör is lehet. A 8-as forma akkor jön létre, amikor a gyűrű belsejét megérinti a sík.
Ezeket a forgástengellyel párhuzamos metszeteket is használhatjuk sliceform modellek készítésére.
Ha leírást is keresünk hozzá, akkor ilyesmi pdf-ket találhatunk a neten több helyen is:
Ezek lapok éppen azok a metszetek, amiket a fentebb lévő animált ábra is mutatott.
De két kört, mint metszetet, máshogy is kaphatunk. Az alábbi ábra körei az ún. Villarceau-körök, melyeket YvonVillarceau(1813-1883) francia csillagászról és matematikusról neveztek el. A múlt század elején igazolták, hogy ezek a körök ugyanakkora szögben metszik a a tórusz összes paralel körét
Ehhez a helyzethez a metsző síknak két helyen
érintenie kell a tórusz belső oldalát, vetítősíkként így láthatjuk ezt a
helyzetet:
Bácskay-Nagy Dávid engedélyével teszem közzé a következő, animált
gif-ből készített videót. Érdemes teljes képernyőn nézni, és a
tanulmányozáshoz bármely pillanatban megállítható.
Pont ábrázolása a kúp felületén: Ha a felületre alkotót illesztünk, akkor azt mindig az alapkör és a csúcspont közé kell rajzolnunk. Egy adott alkotón pont felvétele rendező egyenessel történik.
Pont ábrázolása a kúp felületén: Ha a paralelkört illesztünk a felületre,
akkor azt a forgástengely irányából (felülről) nézve valódi méretű körnek látjuk, míg szemből nézve egy átmérő hosszúságú szakasznak. Az így ábrázolt körvonalon rendezővel jelölhető pont. Az említett paralelkörök felülnézetben koncentrikus köröknek látszanak, de tudjuk, hogy különböző magasságokban vannak.
Pont ábrázolása a henger felületén: Célszerű alkotókat választani, és azon adott magasságban választani a pontot. A hengeralkotók felülnézetben egyetlen pontnak látszanak.
Transzformáció: annak érdekében, a metsző sík és a felület helyzetét jobban lássuk, célszerű olyan transzformációt alkalmazni, melyben a sík vetítősíkká válik. A módszer ismerős, a síklapú testek metszésénél hasonló transzformációt alkalmaztunk.
Szeletelő módszer:a lényege, hogy egy forgásfelületet a tengelyére
merőleges síkkal metszve paralelkört (vagy köröket) kapunk, míg a
felületet metsző síkot metszve egyenest. Minden ilyen szeletelő síkban a
kimetszett alakzatok közös pontjai kijelölhetők.
Ezzel a technikával a metszet nagyon sok pontja előállítható, melyeket görbe vonallal köthetjük össze.
Transzformációs módszer: a metsző síkot vetítősíkká transzformáljuk,
és ezt a transzformációt a felületre is alkalmazzuk. A metsző sík jelöli ki a transzformáció irányát! Ebben a speciális
oldalnézetben könnyen kijelölhetők a metszet
legmagasabban/legalacsonyabban lévő pontjai, de természetesen
általánosabb helyzetű pontok is könnyen szerkeszthetők (különösen a
henger és a kúp esetén).
Milyen pontokat keresünk?
legmagasabban / legalacsonyabban fekvő pontokat (ha léteznek)
a kontúrokon lévő pontokat
a metszet (vagy a vetületének) nevezetes pontjait
és annyi általános helyzetű pontot, hogy a metszet íve könnyen rajzolható legyen.
A szerkesztést könnyítheti, hogy a kúp is és a henger is
egyenesekből álló felület. Egy-egy tetszőlegesen kiválasztott alkotóval
az adott síkot metszve a keletkező görbe egy-egy pontját kapjuk.
Kúp metszete:
Ha olyan síkot veszünk, amely nem halad át a kúp csúcspontján, akkor az alábbi kép elég jól összefoglalja a lehetőségeket: KÖR, ELLIPSZIS, PARABOLA, HIPERBOLA
Forrás: Wikipédia
A fenti képen is jól látszik, hogy az a kép segít a metszet besorolásában, ahol a metsző sík vetítősíknak látszik, és így maga a metszet is egy vonalként jelenik meg. Ha ez nem áll rendelkezésre, akkor transzformációval érdemes előállítani.
KÖR → a forgástengelyre merőleges síkkal
ELLIPSZIS → minden alkotót metsző, de a tengelyre nem merőleges síkkal
PARABOLA → egy alkotóval párhuzamos síkkal
HIPERBOLA → két alkotóval párhuzamos síkkal
Természetesen, ha a metsző sík áthalad a kúp csúcspontján (és metszi is a palástot), akkor alkotópárt kapunk.
A metsző sík változtatásával a metszetek is folyamatosan változnak, amit ez a videó is szemléltet:
Illetve a kúpot az alkotók hosszabbításával könnyen lehet ún. kettős kúppá alakítani. Ezt azért érdemes elképzelni, mert csak ekkor jön létre a hiperbolametszet mindkét ága A metszetek változásait jól szemlélteti az alábbi animált ábra:
Az előbbi ábra bizonyos pillanataiban lehet látni,hogy a metszet lehet alkotópár abban az esetben, a sík áthalad a kúp csúcspontján. Ezt érdemes külön kiemelni:
Ilyen egymás mögötti alkotókat akkor láttunk, amikor a kúp felületén pontokat ábrázoltunk.
Az alkotók segítségével kerül egy síkmetszet megszerkesztésre az alábbi videóban:
Henger metszete:
A henger esetén jóval kevesebb lehetőségünk van: ferde helyzetű síkkal
metszve mindig ellipszist kapunk. Az ellipszis vetülete az 1. képen kör,
míg a 2. képen ellipszis lesz. Az alábbi videóban jól látszik, hogy ha a sík állása egyre jobban eltér a vízszintestől, akkor az ellipszis metszet alakja elkezd nyúlni. Illetve az ellipszis egy része létre sem jön, ha pl. a sík a henger fedőkörébe is bele tud metszeni.
Tapasztalatgyűjtéshez érdemes belenézni az alábbi videóba:
A forgásfelületek elnevezés egy összefoglaló név minden
olyan felületre, amely egy görbe egy adott tengely körüli
megforgatásával keletkezik. A forgatás az egyik gyakran alkalmazott
módszer különböző formák alakjának modellezésére, a szoftverek többnyire
Rotate, Revolution, Revolved Boss/Base parancsokat használnak a
generálásukra.
Felületek előállítását szemléltető eszköz a MoMath matematikai múzeumban.
Ha a megforgatandó görbe alakját figyeljük, akkor
az többnyire egy hullámzó vonal lehet, ha pl. egy váza formáját
keressük. De mérnöki alkalmazásokban alapelemként olyan felületeket
használnak, melyek egyenes vagy kör megforgatásával keletkeznek.
Letölthető anyagok:
A henger és a kúp vonalfelületek, ami azt jelenti, hogy a felület minden
pontján áthalad egy egyenes, vagy annak egy szakasza. Az ábrázolásoknál
kerüljük a végtelenbe futó felületdarabokat, ezért mindig adott
magasságú hengerrel és kúppal fogunk találkozni. Jellemzőjük, hogy síkba
fejthetők, azaz síklapra szerkesztett hálójuk alapján papírmodelljeik
előkészítők.
A henger és a kúp esetén közös tulajdonság az, hogy a felületi pontok keresése kétféle módszerrel valósítható meg: paralelkörrel vagy alkotóval. Az alkotó megjelenítése ahhoz hasonló, amikor a hasáb/gúla oldalélét rajzoltuk meg. És ez nem véletlen, hiszen ha növeljük a hasáb/gúla oldaléleinek és ezzel az oldallapjainak a számát, akkor az oldalfelület elkezd kisimulni, és végül hengert/kúpot kapunk.
A paralelkör megjelenése ahhoz hasonló, amikor a hasábokat/gúlákat egy adott magasságban elmetszettük egy vízszintes síkkal. A henger esetén mindig azonos méretű metszeteket kapunk, míg a kúp esetén a csúcs felé haladva egyre kisebbeket. Ezek a modern mászókák elég jól szemléltik ezt a tényt.
Nagyon fontos, hogy minden felületi ponton át egy alkotó és egy paralelkör vehető fel!
A gömb és a tórusz kör megforgatásával
keletkezik, a gömb esetén a forgástengely áthalad a kör középpontján,
míg a tórusz esetében nem. A felületi pontok megadásakor a meridiánmetszet nem igazán használható, mivel ezek többnyire ellipszisként látszanának. Így csak a forgástengelyre merőleges metszetek, azaz a paralelkörök használhatók.
A tórusz esetén többnyire a lyukas
"változatát" ábrázoljuk, amely hasonlít az úszógumi, biciklibelső
formájához, vagy éppen az amerikai fánk alakjához.
A konzultáción szóba került, hogy a tórusz felületére való illesztés hogyan nézne ki, ha a diasortól eltérően az 1. képről indítanánk. Íme egy kis útmutató:
Továbbá fontos, hogy emlékezzünk arra, hogy a gömb bármely síkmetszete kör, csaknem minden esetben fog körnek látszani. Ha a metsző sík egyik
képsíkkal sem párhuzamos, akkor a metszet vetülete ellipszis lesz.
Ha már a modern mászókákat hívtam segítségül, akkor megmutatom,hogy milyen volt a gyermekkorom játszótere. Ilyen gömbmászókán lógtunk, ha a rakétát a fiúk elfoglalták:
A hosszanti cikkek (olyanok,mint a narancsgerezdek) határai éppen a meridiánmetszetek, és néhány magasságban megvannak a paralelkörök is. A mászóka fokai pedig egyenes szakaszokkal íveket helyettesítettek.
Talán emlékezetes lesz ez a fenti kép, amikor a régi kerékvető követ utólag vágták félbe, hogy a kapu nyílás megfeleljen a mai igényeknek.
Hasonló ötlet 56. oldal feladatának megoldást szemlélteti. Sajnos Önök nem órán látják, hanem csak képen. És mi is a lényeg? Ha egy gömböt egy egyenessel el akarunk metszeni, akkor az egyenesre bárhogy is illesztünk síkot, akkor a gömb metszete éppen a keresett szúráspontokban metszi az egyenest.
Csak nem mindegy, hogy hogyan vesszük fel a síkot! Ha függőleges síkkal metszünk, akkor a metszet könnyen leforgatható. Az alábbi animált ábra éppen a szerkesztést mutatja be:
Ebben az esetben kérdés:
Milyen magasan kell keresni a gömbből függőleges síkkal metszett körközéppontját? Már az almás kép is mutatja, hogy a metszetek nem csúszkálnak el, le, hanem egy adott magasságban maradnak.
Hasznos segítség:
Pethes Endre: 222 Ábrázoló geometriai feladat (IX. és X fejezet),melyeket elérthet ezen a linken
Tehetségműhely
(Békéscsaba, Belvárosi Ált. isk, és Gimn) segédanyaga, amely igazából
egy posztergyűjtemény. Makovecz Benjámin munkája. A forgásfelületek
metszése (és később áthatás is lesz) a 33. oldalon kezdődik.
A fedélidomszerkesztés egy gyakorlatias témakör a síkok metszése és poliéderek áthatása alkalmazására. A feladatunk az lesz, hogy az épületek lefedésekor
használatos tetősíkokat kialakítsuk.
Adottak az egy magasságban lévő ereszvonalak.
Feltételezzük, hogy az ereszvonalakra egyenlő hajlásszögű tetősíkokat illesztünk. A nálunk szokásos síkállás az amelyben a síkok a vízszintes síkkal 45 fokos szöget zárnak be. Mivel egyetlen gyakorlat erejéig foglalkozunk a témakörrel így csak az alapokkal foglalkozunk. A
feladatok egyetlen vetületen megoldhatók, csak a felülnézetet fogjuk
használni.
Ha a tető keresztmetszetét nézzük, akkor az előbb említett 45°-os szögnek annyi hatása van, párhuzamos ereszvonalak esetén a tetősíkok összemetsződéseként kapott gerinc fele akkora magasan lesz az ereszvonal fölött, mint amekkora az ereszvonalak távolsága volt.
Még egy fontos dolgot is észrevehetünk: felülről nézve a gerinc éppen félúton lesz az ereszvonalak között. Geometria nyelvén: középpárhuzamost látunk. A fenti ábrán az is látszik, hogy ha eltérnék a 45%-os hajlásszögtől, akkor csak a tető (gerinc) magasságán változtatnánk, de a gerinc vetülete továbbra is középpárhuzamosként látszana. De vajon mi a helyzet az egymáshoz valamilyen szögben csatlakozó ereszvonalak esetén. Mit látunk a a tetősíkok metszésvonalából az élgerinc és a vápa esetén? Erre mutatok egy példát, amikor az egyik feladatunk modelljét egy 3D nyomtató szeletelőprogramjában megnyitottam, és felszeleteltem:
Felülről nézve a tetősíkokat kirajzoló vonalak úgy látszanak, mintha az ereszvonalat belülről egy vastag filctollal újra és újra körberajzoltuk volna. A modellezésben az ilyen típusú vonalakat offset vonalaknak hívják. De miután az eresz vonaltól mindig ugyanolyan távolságra haladnak, a csúcsokban az irányváltások miatt mindig kirajzolják az élgerincek és vápák vonalát, melyek iránya mindig szögfelező állású lesz.
