2019. április 30., kedd

Forgásfelületek metszése síkkal

Ezen a héten folytatjuk a forgásfelületekkel való ismerkedést, de most a síkkal való metszésre fókuszálunk. Továbbra is a forgástengelyt a K1 képsíkra merőlegesen fogjuk felvenni.

Letölthető anyagok:

 Megismerkedünk az ún. szeletelő módszerrel, amelynek az lesz a lényege, hogy egy forgásfelületet a tengelyére merőleges síkkal  metszve paralelkört (vagy köröket) kapunk, míg a felületet metsző síkot metszve egyenest. Minden ilyen szeletelő síkban a kimetszett alakzatok közös pontjai kijelölhetők. Ezzel a technikával a metszet nagyon sok pontja előállítható, melyeket görbe vonallal köthetjük össze. Egy másik módszer lehet az, hogy a metsző síkot vetítősíkká transzformáljuk, és ezt a transzformációt a felületre is alkalmazzuk.  Ebben a speciális oldalnézetben könnyen kijelölhetők a metszet legmagasabban/legalacsonyabban lévő pontjai, de természetesen általánosabb helyzetű pontok is könnyen szerkeszthetők (különösen a henger és a kúp esetén).
 Minden metszet esetén keressük a
  • legmagasabban / legalacsonyabban fekvő pontokat (ha léteznek)
  • a kontúrokon lévő pontokat
  • a metszet (vagy a vetületének) nevezetes pontjait
  • és annyi általános helyzetű pontot, hogy a metszet íve könnyen rajzolható legyen.
Tehát a használható módszereink:
  • Szeletelő módszer
  • Transzformációs módszer (A metsző sík jelöli ki a transzformáció irányát.)
A szerkesztést könnyítheti, hogy a kúp is és a henger is egyenesekből álló felület. Egy-egy tetszőlegesen kiválasztott alkotóval az adott síkot metszve a keletkező görbe egy-egy pontját kapjuk.
Minden metszet esetén keressük a
  • legmagasabban / legalacsonyabban fekvő pontokat
  • a kontúrokon lévő pontokat
  • a metszet (vagy a vetületének) nevezetes pontjait
  • és annyi általános helyzetű pontot, hogy a metszet íve könnyen rajzolható legyen.
Gömb metszete:
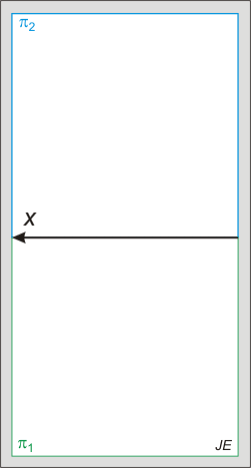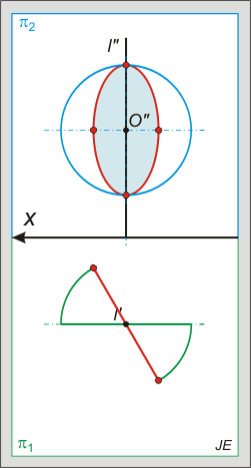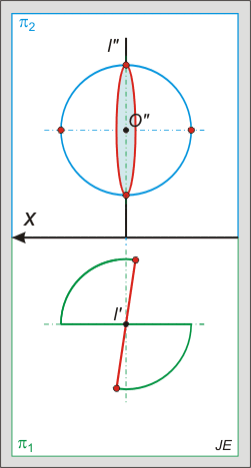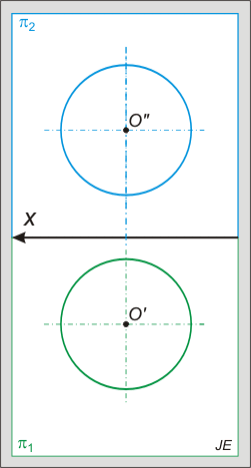
A gömb minden metszete kör, melyet a vetületeken körnek, ellipszisnek, vagy átmérő hosszúságú szakasznak látunk.


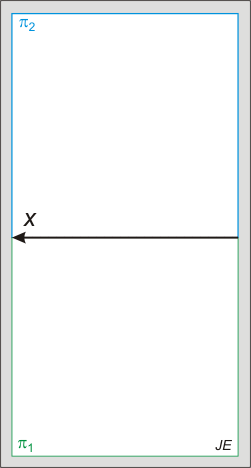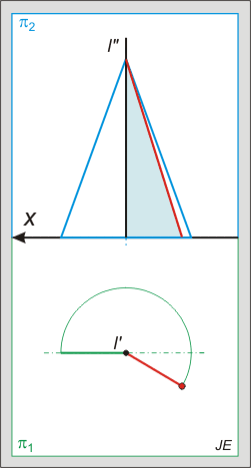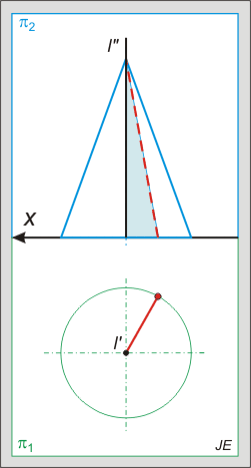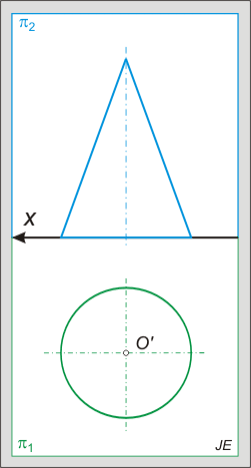
Kúp metszete:
Forrás: Wikipédia

A kúp metszetei csúcspontra nem illeszkedő síkkal metszve:
  • kör (a forgástengelyre merőleges síkkal), 
  • ellipszis (minden alkotót metsző, de a tengelyre nem merőleges síkkal), 
  • parabola (egy alkotóval párhuzamos síkkal), 
  • hiperbola (két alkotóval párhuzamos síkkal)
Természetesen, ha a metsző sík áthalad a kúp csúcspontján (és metszi is a palástot), akkor alkotópárt kapunk.

 A metszetek változásait jól szemlélteti az alábbi animált ábra:


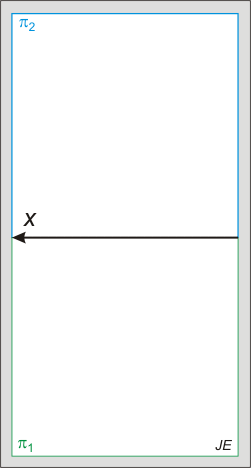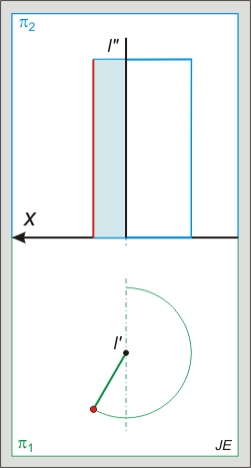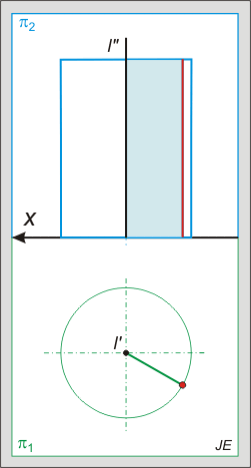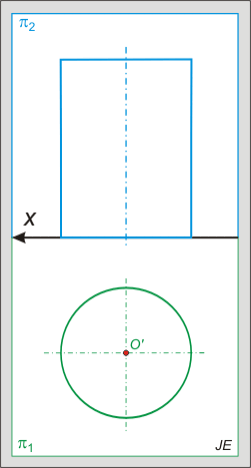
Henger metszete:
A henger esetén jóval kevesebb lehetőségünk van: ferde helyzetű síkkal metszve mindig ellipszist kapunk. Az ellipszis vetülete az 1. képen kör, míg a 2. képen ellipszis lesz.
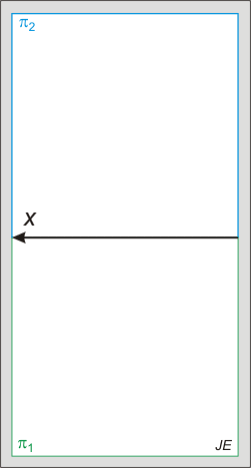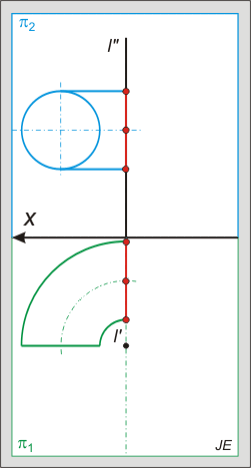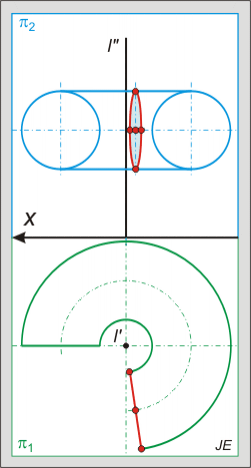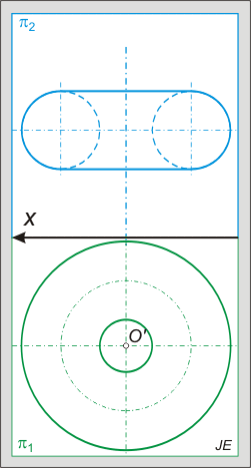
Tórusz metszete:
A tórusszal idő hiányában nem tudunk majd foglalkozni, de érdemes megemlíteni, hogy a metszetei negyedrendű görbék, melyek különböző alakúak lehetnek: "ovális", "piskóta", nyolcas vagy két kör is lehet:

A fenti animált ábrák forrása:
http://fluid.itcmp.pwr.wroc.pl/~eichler/torus-przek2/img/torus-przek-2.gif
http://fluid.itcmp.pwr.wroc.pl/~eichler/torus-przek2/img/tor-prze2.gif
(A könnyebb tanulmányozás érdekében kattintson a linkre és csak az jelenik meg a böngészőben!)

További segédanyag:
Bejegyezte: dátum: Nincsenek megjegyzések:
Címkék: , , , , , ,

2019. április 27., szombat

Forgásfelületek ábrázolása, metszésük egyenessel

A forgásfelületek elnevezés egy összefoglaló név minden olyan felületre, amely egy görbe egy adott tengely körüli megforgatásával keletkezik. A forgatás az egyik gyakran alkalmazott módszer különböző formák alakjának modellezésére, a szoftverek többnyire Rotate, Revolution, Revolved Boss/Base parancsokat használnak a generálásukra.
Felületek előállítását szemléltető eszköz a MoMath matematikai múzeumban.
Ha a megforgatandó görbe alakját figyeljük, akkor az többnyire egy hullámzó vonal lehet, ha pl. egy váza formáját keressük. De mérnöki alkalmazásokban alapelemként olyan felületeket használnak, melyek egyenes vagy kör megforgatásával keletkeznek.
Letölthető anyagok:
A henger és a kúp vonalfelületek, ami azt jelenti, hogy a felület minden pontján áthalad egy egyenes, vagy annak egy szakasza. Az ábrázolásoknál kerüljük a végtelenbe futó felületdarabokat, ezért mindig adott magasságú hengerrel és kúppal fogunk találkozni. Jellemzőjük, hogy síkba fejthetők, azaz síklapra szerkesztett hálójuk alapján papírmodelljeik előkészítők.

A gömb és a tórusz kör megforgatásával keletkezik, a gömb esetén a forgástengely áthalad a kör középpontján, míg a tórusz esetében nem. A felületi pontok beazonosítására figyelni kell, célszerű a  képsíkkal párhuzamos metszetekre illeszteni azokat. A gömb bármely síkmetszete kör, de ha a metsző sík egyik képsíkkal sem párhuzamos, akkor a metszet vetülete ellipszis lesz.
A tórusz esetén többnyire a lyukas "változatát" ábrázoljuk, amely hasonlít az úszógumi, biciklibelső formájához, vagy éppen az amerikai fánk alakjához.
A bejegyzésben található animált gif-ek forrása: http://fluid.itcmp.pwr.wroc.pl/~eichler/tworzace/geom_tworzace_01.html (Készítette: Janusz Eichler)
http://fluid.itcmp.pwr.wroc.pl/~eichler/kula-pr/img/anim-k-pr.gif

További segédanyag: 

  • Kúp és gömb metszése egyenessel.
    Az alábbi animált ábra a gömb és egyenes metszését mutatja, amikor az egyenes első vetítősíkja belemetsz a gömbbe és a metszetet az egyenessel együtt a képsíkba forgatjuk.












  • Az alma, mint modell:
 


  • Pethes Endre: 222 Ábrázoló geometriai feladat (IX. és X fejezet)
  • az olvasnivaló linkje
  • Tehetségműhely (Békéscsaba, Belvárosi Ált. isk, és Gimn) segédanyaga, amely igazából egy posztergyűjtemény. Makovecz Benjámin munkája. A forgásfelületek metszése (és később áthatás is lesz) a 33. oldalon kezdődik.

Bejegyezte: dátum: Nincsenek megjegyzések:
Címkék: , , , ,

2019. április 17., szerda

Gyakorló feladatok a 2. modul pót zh-ja előtt

Az alábbi linken érhetők el:
https://drive.google.com/open?id=1OCYpbZoW_347ykdk7sCJlsn2dKs3Lhas
Bejegyezte: dátum: Nincsenek megjegyzések:

Fedélidomszerkesztés

A fedélidomszerkesztéssel visszatérünk a síkok metszése és poliéderek áthatása témakörhöz. A feladatunk az lesz, hogy az épületek lefedésekor használatos tetősíkokat kialakítsuk. Ennek az lapjait az jelenti, hogy megadjuk az egy magasságban lévő ereszvonalakat, és azokra ráillesztjük a tetősíkokat, melyek a vízszintes síkkal 45 fokos szöget zárnak be. (Ettől persze később le lehet térni, de most az alapoknál kezdjük.)
Szerkesztendők a síkok összemetszésével keletkező gerinc(ek) és élgerincek. A feladatok egyetlen vetületen megoldhatók, csak a felülnézetet fogjuk használni.

Letölthető anyagok

További segédanyag 

Bejegyezte: dátum: Nincsenek megjegyzések:
Címkék: , ,

2019. április 6., szombat

Gúlák és hasábok áthatása 1.

Ezen a héten hasábokat és gúlákat fogunk metszeni egymással. Nem minden helyzettel foglalkozunk, csak azokkal, amikor a hasáb oldalélei képsíkra merőleges helyzetűek. A két poliéder áthatási vonala egy térbeli sokszög lesz, melynek a csúcsait úgy kapjuk, hogy az egyik test éleivel a másik test lapijait metsszük, és fordítva. A kapott pontokat összekötési sorrendjénél figyelnünk kell arra, hogy megfeleljen mindkét test körüljárásának, a testeket alkotó lapok metsződjenek össze és ne lépjük a testek belsejébe.

A feladatot többféleképpen értelmezhetjük: a két test az összemetsződés után egy testté olvad össze, vagy az egyiküket eltávolítva a maradék csonkolt testet jelenítjük meg.

Interaktív ábrák:

Letölthető anyagok:


  • Solidworks-ben készült modell  (tabló, 3 oldalon, különböző helyzetekben mutatja a egyesítést, az egyik hasáb eltávolítását, és a közös részt.)

  • Táblaképek:
  • Megoldott feladat:

További segédanyag

Bejegyezte: dátum: Nincsenek megjegyzések:
Címkék: , , ,
Feliratkozás: Bejegyzések (Atom)