 |
| Felületek előállítását szemléltető eszköz a MoMath matematikai múzeumban. |
Letölthető anyagok:
A henger és a kúp vonalfelületek, ami azt jelenti, hogy a felület minden pontján áthalad egy egyenes, vagy annak egy szakasza. Az ábrázolásoknál kerüljük a végtelenbe futó felületdarabokat, ezért mindig adott magasságú hengerrel és kúppal fogunk találkozni. Jellemzőjük, hogy síkba fejthetők, azaz síklapra szerkesztett hálójuk alapján papírmodelljeik előkészítők.
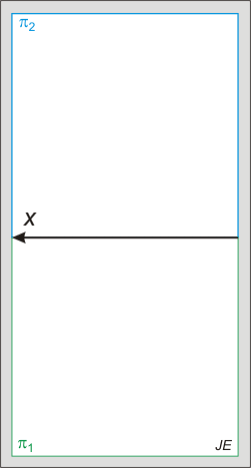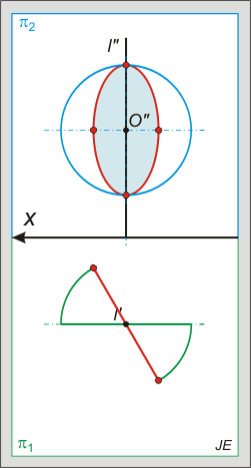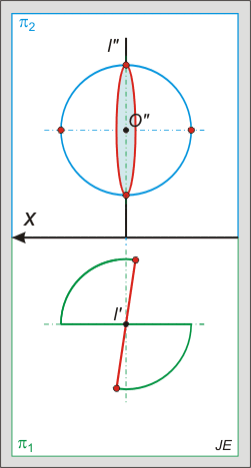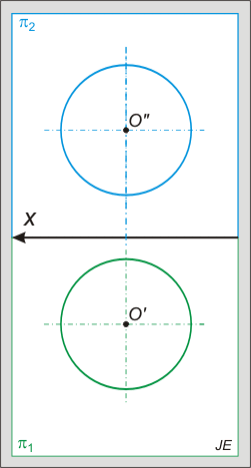
A gömb és a tórusz kör megforgatásával keletkezik, a gömb esetén a forgástengely áthalad a kör középpontján, míg a tórusz esetében nem. A felületi pontok beazonosítására figyelni kell, célszerű a képsíkkal párhuzamos metszetekre illeszteni azokat. A gömb bármely síkmetszete kör, de ha a metsző sík egyik képsíkkal sem párhuzamos, akkor a metszet vetülete ellipszis lesz.
A tórusz esetén többnyire a lyukas "változatát" ábrázoljuk, amely hasonlít az úszógumi, biciklibelső formájához, vagy éppen az amerikai fánk alakjához.
 |
| http://fluid.itcmp.pwr.wroc.pl/~eichler/kula-pr/img/anim-k-pr.gif |
További segédanyag:
- Kúp és gömb metszése egyenessel.
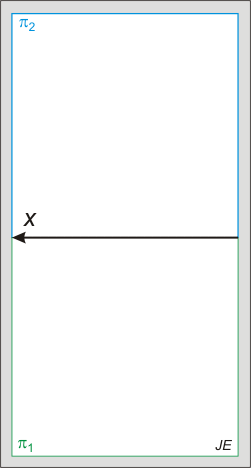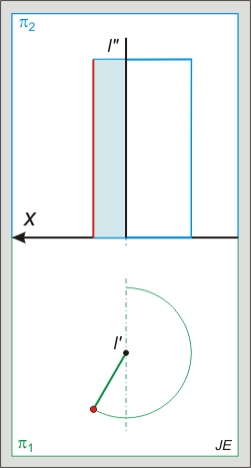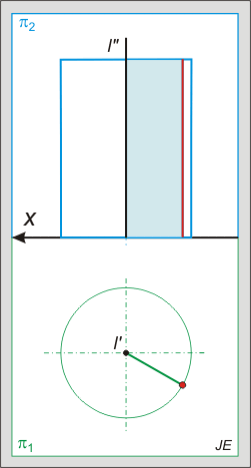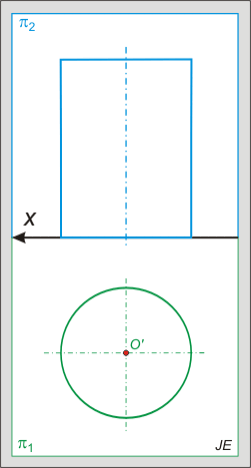
Az alábbi animált ábra a gömb és egyenes metszését mutatja, amikor az egyenes első vetítősíkja belemetsz a gömbbe és a metszetet az egyenessel együtt a képsíkba forgatjuk.
- Gömb metszése vetítősíkkal, Borda Tiborné munkája, letölthető a http://www.stromfeld.starjan.hu oldalról (tanári letöltések, Borda Tiborné,10B eléréssel), feladatlap
- Az alma, mint modell:
- Pethes Endre: 222 Ábrázoló geometriai feladat (IX. és X fejezet)
- az olvasnivaló linkje
- Tehetségműhely (Békéscsaba, Belvárosi Ált. isk, és Gimn) segédanyaga, amely igazából egy posztergyűjtemény. Makovecz Benjámin munkája. A forgásfelületek metszése (és később áthatás is lesz) a 33. oldalon kezdődik.
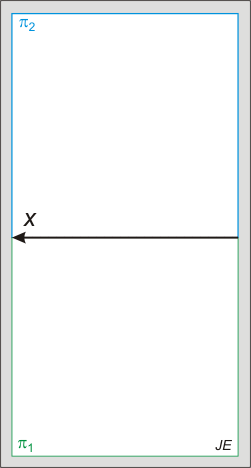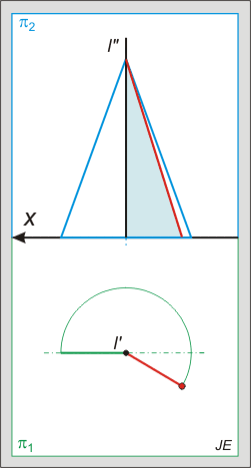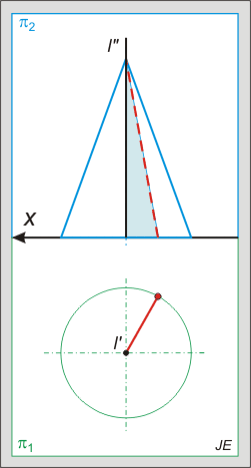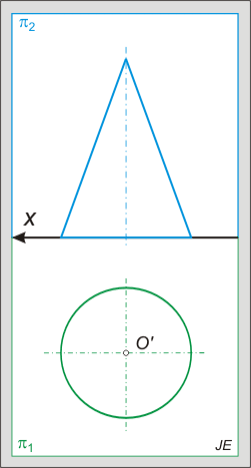

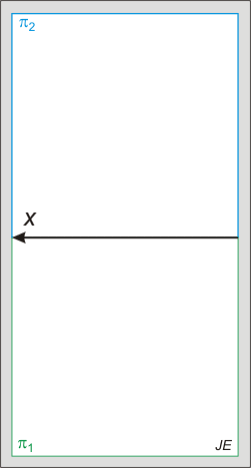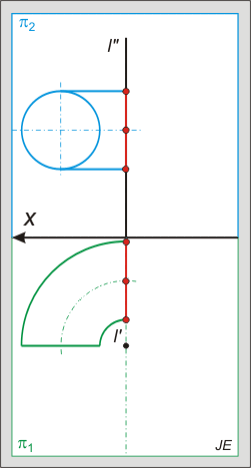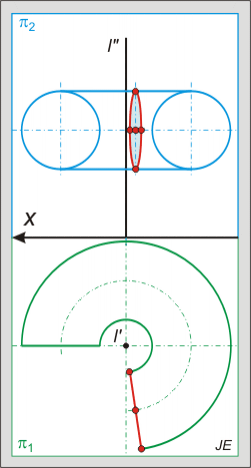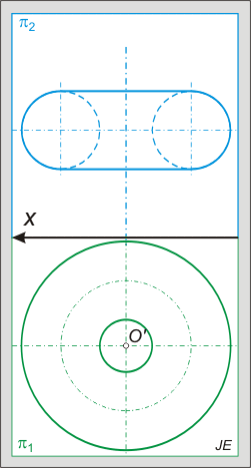


Nincsenek megjegyzések:
Megjegyzés küldése