Hasáb és gúla áthatása

Hasábok áthatása

Síklapú testek áthatása

Ezen a héten hasábokat és gúlákat fogunk metszeni egymással. Nem minden helyzettel foglalkozunk, csak azokkal, amikor a hasáb oldalélei képsíkra merőleges helyzetűek. A két poliéder áthatási vonala egy térbeli sokszög lesz, melynek a csúcsait úgy kapjuk, hogy az egyik test éleivel a másik test lapijait metsszük, és fordítva. A kapott pontokat összekötési sorrendjénél figyelnünk kell arra, hogy megfeleljen mindkét test körüljárásának, a testeket alkotó lapok metsződjenek össze és ne lépjük a testek belsejébe.

A feladatot többféleképpen értelmezhetjük: a két test az összemetsződés után egy testté olvad össze, vagy az egyiküket eltávolítva a maradék csonkolt testet jelenítjük meg.

Letölthető anyagok:

• Diasor pdf-ben, és a folytatása
• Feladatlapok: a munkafüzet 29-35. oldala
• Házi feladat (2.-3. oldal)
• Segédábrák a  láthatósághoz.

További segédanyag

• Szemléltető videók a blog Szemléltető videók oldalán találhatóak.
• Két hasáb áthatása lépésenként megmutatva
• Forgatható ábra 1.
• Forgatható ábra 2.
• Forgatható ábra 3.
• Forgatható ábra 4.
• Hasábok áthatása (unió, különbségek)  
• Gúla-hasáb áthatás (unió, különbség)

Síklapú testek ábrázolása, metszésük egyenessel, síkkal.

Ezen a héten síklap testek közül a hasábokkal és a gúlákkal kezdünk ismerkedni. A (többnyire az első képsíkon álló) testeket egyenesekkel és síkokkal (síklapokkal) fogjuk elmetszeni.

Ehhez nem kell mást ismerni, mint a korábbiakban megtanult döféspont és metszésvonal szerkesztést. Az elemek speciális helyzetének felismerése segíti, és gyorsítja a szerkesztést. A feladatok azért tűnnek nehezebbnek, mert egy ábrában több egyenes és több sík szerepel, és el kell igazodnunk közöttük. Most az eddigieknél is jobban kell használnunk a képzelőerőnket.

Letölthető anyagok:

• Diasor pdf-ben.
• Feladatlapok: a munkafüzet 24-28. oldala
• Házi feladat (1. oldal)

Vázlatok:

További segédanyag 

• Modellek interaktív frame-ben:  gúla metszése, még egy gúla,  hasáb metszése)
• gúla metszése (dinamikus html oldal, Németh László)
• gúla metszése síklappal  (dinamikus html oldal, Németh László)
• kidolgozott feladatok
• hallgatói munkák 1999-2000
• A bemutatott papírmodellek

 

Sík leforgatása

Egy olyan módszerrel ismerkedünk meg, amely során nem változtatjuk meg a nézőpontunkat, hanem az alakzatot hozzuk egy számunkra kedvezőbb helyzetbe: ez lesz a sík képsíkkal párhuzamos helyzetbe forgatása.

Az ábra a sík egy pontjának leforgatását szemlélteti

 A képsíkkal (K1 képsíkkal) párhuzamos helyzet azért előnyös, mert ekkor felülnézetben a sík alakzatai közötti méretekkel kapcsolatos minden információ leolvasható lesz.
A szerkesztéseink lényege az lesz, hogy egy síkot annak egy első fővonala körül K1-gyel párhuzamos helyzetbe forgatunk. Ezzel egy síkbeli alakzat első és forgatott képe kötött létrejön egy olyan kapcsolat, amelyre a következők teljesülnek:

• A forgástengelyként használt fővonal a forgás során helyben pontonként helyben marad, vagyis minden pontjának első és forgatott képe egybeesik.
• Minden síkbeli pont első és forgatott képét egy olyan vonal köti össze, amely merőleges a fővonal első képére.
• Ha egy síkbeli egyenes elmetszi a forgástengelyt, akkor a forgatott képe ugyanott metszi azt. 
• Ha egy síkbeli egyenes párhuzamos a forgástengellyel, akkor a forgatott kép is párhuzamos lesz a tengellyel. (A forgatás során végi megőrződik a párhuzamosság!)
• Ha az első és forgatott képet, melyek a tengelyeként használt fővonalon csatlakoznak egymáshoz, jobban megfigyeljük, akkor az ábra nagyon hasonlít a tengelyes szimmetriához, DE attól annyiban tér el, hogy az alakzat első képe kissé "össze van nyomva" a forgástengelyre merőleges irányban.

Ez a fenti leképezés a geometriában a tengelyes affinitás, amelyben az egymásnak megfelelő pontokat a tengelyre merőleges egyenesek kötik össze. (ortogonális tengelyes affinitás)

Letölthető anyagok:

• Diasor pdf-ben
• Feladatlapok: a munkafüzet 19-24. oldala
• HÁZI FELADAT (3. oldal)

Képek az órai modellről:

A gyakorlat táblaképei

Munkafüzet 24. oldal feladata.
Az adott síkot leforgatjuk, és a leforgatott részen megszerkesztjük a feladatban kért négyzetet.

Ezután a négyzet első képét szerkesztjük a forgatás visszafelé történő alkalmazásával. Ehhez a négyzet egy szemköztes oldalpárját hosszabbítottuk meg a forgatás tengelyéig. A négyzet első képe paralelogramma lesz.

A második kép szerkesztése a síkra való illesztésekkel történik. Azokat a szemköztes oldalegyeneseket használhatjuk most is, amivel az első képet szerkesztettük. a jobboldali ábrán végül megmutattam, hogy hogyan néz ki a feladat másik megoldása, amikor az a egyenes másik oldalán vesszük fel a négyzetet. Ennek az a "baja", hogy a forgatott képe elmetszi a forgatás tengelyét, ezért az első képe is átlóg a nyomvonal másik oldalára, és ezzel fedésbe kerül a leforgatott és az első kép. Ennek következménye, hogy egy csúcspont a második képen az x12 alá fog kerülni.
(Ha van lehetőségünk választani, akkor célszerű kerülni az ilyen helyzeteket.)

További segédanyag

• A modellekről készült képek kiegészítésekkel nagyobb méretben

A képsíkrendszer transzformációja

Az ábrázolási rendszerünk meghatározza, hogy egy tárgyat, alakzatot honnan nézhetünk. A Monge-féle kétképsíkos eljárásban mindig a képsíkra merőleges irányból készült vetületekkel találkozunk. Felmerülhet a kérdés: Jó ez minden esetben?
A válasz természetesen nem. Előfordulhat, hogy a könnyen szerkeszthető nézet helyett inkább a szemléletes mellett döntenénk. De hogyan juthatunk el az egyik képből a másikba? Ez az út a képsíkrendszer transzformációja: amely röviden fogalmazva újabb vetület(ek) szerkesztését jelenti az előző kép(ek) felhasználásával.

Letölthető anyagok:

• Diasor pdf-ben
• Feladatlapok: munkafüzet 12-18. oldala
• HÁZI FELADAT (1-2. oldal)
  

Segédanyagok, feladatok:

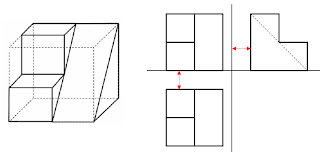
• Gondolkodjunk el azon, hogy milyen testeknek lehet a vetülete szemből nézve is, és felülről nézve is négyzet? Milyen oldalnézetek lehetségesek?
• Forgatható 3D ábra a transzformációs feladathoz:
  https://www.tinkercad.com/things/cEAXwJWjULU#/
• Táblaképek A gyakorlaton a szerkesztés folyamatát is sikerült megörökíteni:

• Feladatok gyakorlásra
• 
  

Síkok és egyenesek metszése

Ezen a héten az illeszkedési feladatokra alapozva metszési feladatokat fogunk megoldani: egyenes és sík metszéspontját, vagy két sík metszésvonalát fogjuk szerkeszteni.

Forrás (már nem érhető el):
http://old.eng.unideb.hu/mat/hun/projektek/animaciok/sikok.html

 Ha valamelyik térelem vetítő helyzetben van, akkor a metszés könnyen szerkeszthető, "cserébe" nem olyan szemléletes a kép.
Egyenes és sík metszése:

Általános helyzetű térelemek esetében a fedő egyenespár módszerét alkalmazhatjuk. Ennek az lesz a lényege, hogy az elképzeljük az egyenes egyik vetítősíkját, és azzal az adott síkba metszünk. Ekkor egy olyan egyenest kapunk, amely az adott egyenes alatt/fölött halad, és közben át is metszi azt.

Ez ábrán a V1 első vetítősíkot választottam, amely az m egyenesben metszi a háromszöglap síkját. Az első képen (felülnézetben) az adott egyenes és az m egyenes ugyanabban  a vonalban látszik, míg a 2. képen (szemből nézetben) azt látjuk, hogy hogy az e és m egyenesek metszőek. Ezt a metsző helyzetet természetesen bármely oldalnézet is megmutatná

Két sík metszése:

A tétben egy egyenest két pontja egyértelműen meghatározza. Így, ha két síkot el kell metszenünk, akkor két db közös pontot fogunk szerkeszteni a fenti módszer segítségével, és azokat össze fogjuk kötni. Ehhez bármely két közös pont felhasználható, de fontos, hogy ha a többit is meghatároznánk, akkor azok is illeszkednének a metszésvonalra.

Láthatóság:

Minden metszési feladatot szemléletessé fogunk tenni az ún. láthatóság szerinti kihúzással. Az adott síkot/síkokat síklapokként képzeljük. Kiválasztjuk azokat szakaszokat és területeket, melyek egy adott vetületben takarásban vannak, és szaggatott vonallal jelöljük azokat. A látható szakaszokat folyamatos vonallal jelöljük, általában vastagabb vonallal, vagy ahogy a diákon is látható színes vonallal. Az eljárás végén egy szemléletes képet kapunk az alakzatok átmetsződéséről.

Letölthető anyagok:

• Diasor pdf-ben
• Feladatlapok:a munkafüzet 8-11. oldala
• HÁZI FELADAT

Táblai feladatmegoldások a korábbi évekből:

További segédanyag

• Egy feladat  megoldása lépésenként megmutatva
• http://users.atw.hu/mageptech/Tantargyak/muszakiabr/metsze.jpg
• Sulinet tudásbázis (link)
   
  

Illeszkedés

A térelemek ábrázolása során gyakran előfordul az, hogy illeszkedő térelemeket kell ábrázolnunk. Az illeszkedésnek vannak látható feltételei, melyekre ezen a héten több figyelmet fogunk szánni. A főbb tudnivalók vázlatosan:

• Pont és egyenes illeszkedése:
  Jusson eszünkbe, hogy ha egy drótszálra gyöngyöt fűzünk, akkor  bárhonnan is nézzük, mindig azt látjuk, hogy a gyöngy a szálon van.
  

  

  http://meska.hu/img/blog/post_9ee0366ea5282d16251d4f9633d383a4639.jpg

  Ábrázoláskor fontos, hogy mindkét képen látható legyen az "illeszkedik" helyzet, vagyis a pont első képe az egyenes első képére, a pont második képe az egyenes második képére illeszkedjen, és természetesen a pont képeit rendezővel tudjuk összekötni.  
• Egyenes és sík illeszkedése:
  A természetben a pókháló emlékeztet erre legjobban. A pók úgy tud a tartószálak által feszített felületen (ez gyakran síknak vehető) maradni, ha a fő szálak közé újabb szálakat sző. Ezek a szálak gyakran megereszkednek, de az elvet jól szemléltetik.
  

  

  http://7-themes.com/data_images/out/24/6849391-spider-web.jpg

  Ábrázoláskor egy egyenes síkra való illesztése már bonyolultabb, ugyanis az már ismert elemekhez kell "ragasztanunk" az újabbat. A síkot úgy kell tekinteni, mintha egy átlátszó fólia lenne, amelyre rajzolhatunk. Metsző egyenes párral adtunk meg egy síkra minden újabb egyenes az adott egyenesekkel alkotott metszéspontjai által rögzíthető! Adott egyenesek egyikével párhuzamos egyenes pedig a másikkal alkotott metszéspont és a párhuzamosság által illeszthető.
• Pont és sík illesztése:
  Ha az előbbi pókháló szálain kicsapódik a pára, akkor az előbbi két esetünk kombinálódik. A vízcsepp csak akkor tud a háló síkjában maradni, ha a szálakon van.

  

  http://farm3.static.flickr.com/2533/3838029983_094c7feece_o.jpg

  A pont síkra történő illesztése viszont összetettebb. Az új pontot a sík régi adataihoz csak egy újabb egyenes segítségével tudjuk kötni. Vagyis először egy új egyenest illesztünk a síkra, majd azon jelöljük ki az új pontot.

Természetesen ezek általános elvek, a speciális helyzetű elemek esetében eleve egyszerűsödnek, más esetekben nekünk kell keresni az egyszerűsítés lehetőségét.

Letölthető anyagok:

• Diasor pdf-ben
• Feladatlapok: a munkafüzet 4-7. oldala
• HÁZI FELADAT

További segédanyag

• Papp Ildikó: Műszaki ábrázolás MFK-s hallgatóknak  12.-14. o.
• De minden más ábrgeom könyv bevezető fejezete jó.

Kétképsíkos ábrázolási rendszer (Monge-rendszer)

Ezen a héten a térelemek ábrázolásával foglalkozunk. Megismerjük a Monge-rendszert, amelyben egyszerre kell dolgoznunk egy alakzat elöl- és felülnézetével. A vetületek helyzetéből kell majd következtetnünk az alakzatok térbeli helyzetére, a képsíkokhoz viszonyított helyzetükre.

• Alapfogalmak: képsíkrendszer, rendező, térnegyedek, pontok ábrázolása a térnegyedekben, pont távolsága a képsíkoktól.
• Síkok megadása különböző elemekkel (3 általános helyzetű ponttal, metsző egyenespárral, párhuzamos egyenespárral, pont és rá nem illeszkedő egyenessel), síkok helyzete a képsírendszerben, térbeli helyzet visszaállítása, modellezés.

Forrás: Sokszínű matematika 5. osztály

• Meg kell említenünk, hogy mi az európai ábrázolási rendszert fogjuk használni. Az alakzatot egymásra merőleges képsíkok által határol „szobasarokba” helyezzük, majd a síkokra merőlegesen vetítjük. A vetítés után a képsíkokat kihajtogatjuk a vetületekkel együtt. A vetítések során fontos, hogy a sorrend minden esetben: szemlélő – alakzat – képsík.
  Általában következő vetületek készülnek: elölnézet, felülnézet, oldalnézet (balnézet).
  Szükség esetén kiegészíthető a rendszer a teljes „bedobozoláshoz” a hiányzó három síkkal, melyek a következő képek keletkeznek: alulnézet, hátulnézet, oldalnézet (jobbnézet).
• Csonkolt kocka axonometrikus képének felhasználásával készítse el a vetületi ábrákat! (felülnézet, elölnézet, oldalnézet) A vetületei ábrákon a takart vonalakat is tüntesse fel vékony szaggatott vonallal.

 

Letölthető anyagok:

• Diasor pdf-ben
• Feladatlapok: a munkafüzet 2-3. oldala

További segédanyag

• Papp Ildikó: Műszaki ábrázolás MFK-s hallgatóknak segédlet 1-11 o.
• De minden más ábrgeom könyv bevezető fejezete jó.
• Ábragyűjtemény az axonometrikus kép - vetületi ábrázolás gyakorlásához
  (A speciális helyzetű éleket, lapokat érdemes a vetületi ábrában is beazonosítani!)
• Ester Alonso Geogebra feladatlapjai
  
• Külföldi példák: Egy spanyol kurzusra készült személtető modellekből mutatok példát. Jól láthatók rajta a vetítő egyenesek, vetületek.  További képek ebben a galériában érhetők el. A képeket a Pinterestre Mariana Martínez Castrejón és Engracia Ramirez felhasználók töltötték fel.

Forrás: Pinterest

•  Csonkolt alakzat kialakítása vágással (forrás)

Nyári szünetre mentünk

és a körzőt, vonalzót, na és persze a  tankönyveket a következőkre cseréljük:

Mindenkinek kellemes pihenést kívánok!

Boltozat szemléltetésére naranccsal

Néhány fázisfotót mutatok, hogyan érdemes az ívek lefutását tanulmányozni: