Nyári szünetre megyünk

Még tart a vizsgaidőszak és igazából még nem kezdődött el a vakáció. De kurzust lezártuk és a blog nyári szünetre készül. A következő bejegyzések szeptember elején várhatók.
Mindenkinek kellemes nyarat kívánok!

Boltozatok szerkesztése

Az utolsó témánk a boltozatszerkesztés, melyben hengereket és gömböket használunk különböző terek lefedésére.  A legegyszerűbb a téglalap alakú terület lefedésére használatos dongaboltozat, illetve a kör alakú terület lefedésére használatos gömbkupola. Először a félgömb vágásával nyerjük a cseh- és a csehsüvegboltozatot, majd a félhengerek áthatásával a kereszt- és kolostorboltozatot. De ezek csak az alapot adják az összetett boltozatok kialakításához.Szabálytalan terek lefedésével és különböző szélességű folyosókat lefedő dongaboltozatok összemetsződésével találkozhatunk.

A félgömbből síkmetszéssel nyert boltozatok:

Cseh boltozat	Cseh süvegboltozat	Csegelyes kupola

Hengerből áthatással nyert boltozatok:

Keresztboltozat	Kolostorboltozat

Szükségesek:

• Diasor   
• Munkafüzet 73-77. oldalai

Egy kis konyhai szemléltetés: Boltozat szemléltetése naranccsal 

Szemléltető videók:

További segédanyag: 

• Hallgatói munkák
• A GeomTech3D projekt keretében készült segédanyag (a szöveg horvát nyelvű, de az ábrák szemléletesek.) 
• A dongaboltozatok áthatásával keletkező boltozat szerkesztésének lépései táblaképek alapján:
  https://drive.google.com/open?id=0B_XPtCdn7YKzUHVLb2c4bldTd1U
• Megoldott feladatok (Egy szabálytalan forma fölé emelt csehboltozat (2014)):

Az ívek fontos pontjai a kezdő- és végpontok, illetve a felezési pont. Pl.: Az 567 ív esetén az 5'7' szakasz egy félkör alakú homlokív vetülete, azaz egy átmérő  hosszúságú vetület. Ennek a fele az ív sugara (kapcsos zárójel).
Az 5" és 7" rendezővel jelölhető ki az x12-n,  a 6" a rendezőn sugárnyi magasan van (kapcsos zárójel).
B, J kontúrpontok: Itt a térben a K2-vel párhuzamos főkör felső fele és az 567, 781 ívek metszik egymást. (mindhárom kör függőleges síkban van) 
A közös pontok az első képen a B', J' kijelölhetők, a második képen rendezőkkel adhatók meg.
A B" és J" pontokban a félellipszisek és a félkör érintkezni fognak.
A táblaképen az 187 homlokívet a képsíkba forgattunk azzal a céllal, hogy az ív további pontjait meg tudjuk határozni a 2. képen.
Kijelölünk egy magasságot (kék kettős nyíl) a forgatott képen egy 8'1'-vel párhuzamos egyenessel,
ez az egyenes a forgatott kört P-ben és Q-ban metszi. P', Q' merőleges állítással, P" Q" a rendezőn a választott magasságban (kék kettős nyíl) szerkeszthető. 

Táblakép 2015-ből egy ív beforgatásával:

Forgásfelületek áthatása

 Letölthető anyagok:

• Diasor és Diasor
• Munkafüzet 64-72. oldalai

Ebben a témakörben 1 gyakorlat erejéig forgásfelületek áthatásával foglalkozunk. Ez a témakör a korábbi síklapú testek áthatása témakör továbbgondolása, ugyanis legvégül minden forgásfelület (de a szépen hullámzó ún. szabad formájú felületek is) poliéderekkel vannak közelítve a megjelenítések vagy az előállítások során. Ahhoz, hogy kezelhetők legyenek, bizonyos metszeteket kell ismernünk.
Az áthatásszerkesztés módszerei és ötletei attól függhetnek, hogy a felületek tengelyei egymáshoz képest hogyan helyezkednek el. Ezen a gyakorlaton az egybeeső és a párhuzamos tengelyű forgásfelületekkel foglalkozunk

Egybeeső tengelyek esetén a felületek  paralel körökben metszik egymást. A meridiángörbék közös pontjait kell keresni, ezek forgatásával nyerjük az áthatást adó kört (köröket).

Párhuzamos tengelyek esetén megadott felületeket a tengelyükre merőlegesen szeleteljük. Egy ilyen szeletelősíkban mindkét felület egy-egy (ritkán több) paralel köre rajzolódik ki. Ezek közös pontjai az áthatási görbe pontjai lesznek. Célszerű elég sűrűn szeletelni, hogy a kapott pontok minél jobban megmutassák az áthatási görbe formáját. 
Az áthatási görbének vannak szélső helyzetű (legmagasabban, legalacsonyabban lévő), kontúron lévő és a felületek közös szimmetriasíkjában lévő pontjai, ezeket jól választott szeletelősíkokkal tudjuk meghatározni. Ilyen helyzetet szemléltet az alábbi videó, amely 66. oldal feladatának a modelljén mutatja be a szeletelő eljárást.

 A 67. oldal: feladatának különlegessége, hogy a gömb érinti a kúpot. Ez azért érdekes helyzet, mert ebben a pontban kialakul egy ún. kettőspont. A görbén végighaladva ezen a ponton irányváltás nélkül jutunk át. Az alábbi képek ezt a helyzetet szemléltetik többféle nézőpontól. (További képek a feladat modelljéről)
A bal oldali ábra a modellt, a jobb oldalin a felületek kikapcsolva, csak a kontúrok, perem, és az áthatási görbe látszik:

Ha a modell belülről üreges, akkor beleláthatunk, és ekkor onnan figyelhető meg az áthatás vonala. A másik képen szeletelés egy lépése látszik: mindkét testből paralel kört metszünk, ezek közös pontjai az áthatási görbe két pontját adják.

Amikor a két felület forgástengelye metsző vagy kitérő helyzetben van egymáshoz képest, akkor a módszerek és ötletek is alkalmazkodnak ezekhez a helyzetekhez, bár az is igaz, teljesen általános helyzetekkel nem fogunk találkozni.
Pl. A forgástengelyek egymásra merőleges helyzetben lesznek. Ez egy igen fontos könnyítés, mert így egy fekvő helyzetben lévő henger vízszintes síkokkal is könnyen szerkeszthető metszeteket ad.
A módszerünk:

SZELETELÉS !!!

A kurzus végén már nem azon kell gondolkodni, hogy mi a szeletelés, hanem alkalmazni azt SOKSZOR. Ezzel lehet biztosítani, hogy nagyon közel lesznek megszerkesztett pontok, amiket össze lehet/kell kötni. De látatlanban nem lehet megtanulni azt, hogy milyen is lesz egy áthatási vonal futása, ezért lássunk néhány példát:

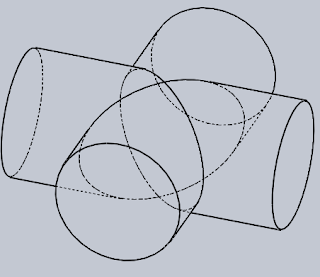
Ez a két henger egyenlő sugarú és a tengelyeik metsző helyzetben vannak. Alapban bárhogy elhelyezkedhetnek a térben, ezeken a képeken "fekvő" helyzetben vannak. Vagyis így, ahogy vannak, le lehet tenni őket az asztalra és egy lappal le lehet fedni őket. A geometria nyelvén ez azt jelenti, hogy alulról és felülről ugyanaz a síkpár érinti mindkét hengert → a legalsó és a legfelső alkotók metszéspontjaiban  a hengerek érintik egymást, és az árhatási vonal szétesik két ellipszisre. Ezek vonala a fenti képeken nagyon szépen kirajzolódik. Az ellipszisek síkjai egymásra merőlegesek, felülről nézve X-et formáznak. Ezzel a helyezettel még fogunk találkozni a Boltozatok témánál.

Ha az előbbi helyzeten csak annyit változtatunk, hogy csökkentjük a sugarát, akkor a fentebb említett érintkezést alul is és felül is elrontjuk. Egyszerűen a sárga henger vastagabb, a szürke vékonyabb és csak amiatt marad meg a levegőben, mert átdugtuk a sárga hengeren.

Ilyenkor az áthatásvonala két különálló zárt vonalból áll. Ezek szimmetrikusan helyezkednek el és kb olyasmi tekeredésük van, mint a Pringles csipsz peremének.

A peremet kell figyelni, és nem a csipsz felületét! A lényeg, hajlása van felfelé és lefelé is.

Hogyan érdemes szeletelni?


Az előbbi esetekben a forgástengelyek síkja mindkét felületnek szimmetriasíkja. Egy ilyen szeletelő síkban a hengerekből egy-egy alkotópárt találunk, melyek összesen 4 metszéspontot határoznak meg.

 Vagyis a teendő: minél többször felvenni ilyen szeletelő síkot és négyesével megszerkeszteni a pontokat. Gyors és egyszerű eljárás! A munkafüzet 69. oldalán a vastagabb henger álló helyzetben van és a vékonyabb vízszintesen fúrja át. Ez azt jelenti, hogy ott a szeletelősíkjaink függőleges helyzetűek leszek, egészen pontosan a K2-velpárhuzamosak.

Az előbbi hengereket szeletelhetjük az egyik tengelyre merőlegesen is. Ekkor az egyik hengerből paralel kört, a másikból alkotópárt metszünk. Az egy szeletelősíkban lévő metszetek közös pontjai kijelölhetők. Valahogy így: 

Ez is gyors módszer, mint ahogy a képen is látszik, egy lépésben 4 pontot tudunk előállítani.

Ha a tengelyeket a metsző helyzetből elmozdítjuk, akkor kitérő tengelyeket kapunk. Kitérő tengelyek esetén általában az egyik tengelyre merőlegesen érdemes szeletelni. Ebben a szemléltető példában egy fekvő henger és függőleges tengelyű kúp került áthatásra. A szerkesztést megkönnyíti, ha a hengert vetítő helyzetűvé transzformáljuk. És ebben a helyzetben a szeletelést vízszintes síkokkal érdemes elvégezni, mert akkor a kúpból kimetszett kört két hengeralkotóval kell összemetszeni.

A 72. oldal feladatában a henger a K2 képsíkra merőleges, így nem kell transzformálni.

Itt a szerkesztés lépései talán jobban látszanak:

Találtam egy galériát, ahol a 4 évvel ezelőtti gyakorlaton a táblaképeket megőriztem. Így a  szerkesztés néhány lépése követhető itt: https://drive.google.com/open?id=0B_XPtCdn7YKzcnNpdXpIMXRjSDQ

További segédanyag:

• Részlet Pethes Endre: 222 ábrázoló geometria feladat c. könyvéből. (XI. fejezet)
• gyakorló feladatok
• Illetve a jobb oldalon ajánlott irodalomból az Ábrázoló geometria szemléletesen című könyv megfelelő fejezete
• hallgatói munkák

 Vendégposztok: 

• Hengerek áthatása,  
• Kúpok és hengerek áthatása