Kezdődik a nyári szünet!

Mindenkinek kellemes nyarat kívánok!

Fedélidomok szerkesztése

A fedélidomszerkesztés egy gyakorlatias témakör a síkok metszése és poliéderek áthatása alkalmazására. A feladatunk az lesz, hogy az épületek lefedésekor használatos tetősíkokat kialakítsuk.

Adottak az egy magasságban lévő ereszvonalak.
Feltételezzük, hogy az ereszvonalakra egyenlő hajlásszögű tetősíkokat illesztünk. A nálunk szokásos síkállás az amelyben a síkok a vízszintes síkkal 45 fokos szöget zárnak be. Mivel egyetlen gyakorlat erejéig foglalkozunk a témakörrel így csak az alapokkal foglalkozunk. A feladatok egyetlen vetületen megoldhatók, csak a felülnézetet fogjuk használni.
Ha a tető keresztmetszetét nézzük, akkor az előbb említett 45°-os szögnek annyi hatása van, párhuzamos ereszvonalak esetén a tetősíkok összemetsződéseként kapott gerinc fele akkora magasan lesz az ereszvonal fölött, mint amekkora az ereszvonalak távolsága volt.

Még egy fontos dolgot is észrevehetünk: felülről nézve a gerinc éppen félúton lesz az ereszvonalak között. Geometria nyelvén: középpárhuzamost látunk. A fenti ábrán az is látszik, hogy ha eltérnék a 45%-os hajlásszögtől, akkor csak a tető (gerinc) magasságán változtatnánk, de a gerinc vetülete továbbra is középpárhuzamosként látszana. De vajon mi a helyzet az egymáshoz valamilyen szögben csatlakozó ereszvonalak esetén. Mit látunk a a tetősíkok metszésvonalából az élgerinc és a vápa esetén? Erre mutatok egy példát, amikor az egyik feladatunk modelljét egy 3D nyomtató szeletelőprogramjában megnyitottam, és felszeleteltem:

Felülről nézve a tetősíkokat kirajzoló vonalak úgy látszanak, mintha az ereszvonalat belülről egy vastag filctollal újra és újra körberajzoltuk volna. A modellezésben az ilyen típusú vonalakat offset vonalaknak hívják. De miután az eresz vonaltól mindig ugyanolyan távolságra haladnak, a csúcsokban az irányváltások miatt mindig kirajzolják az élgerincek és vápák vonalát, melyek iránya mindig szögfelező állású lesz.

 

 

Letölthető anyagok

• Diasor   
• Munkafüzet2025, 40-44. o.
• Fedélidom szerkesztés (segédlet)

További segédanyag

• Fedélidomok_hallgatói munkák
• Néhány feladat megoldása+1 lap 
• Gyakorló feladatok - fedélidom  
• Fedélidomok

Boltozatok szerkesztése

Az utolsó témánk a boltozatszerkesztés, melyben hengereket és gömböket használunk különböző terek lefedésére.  A legegyszerűbb a téglalap alakú terület lefedésére használatos dongaboltozat, illetve a kör alakú terület lefedésére használatos gömbkupola. Először a félgömb vágásával nyerjük a cseh- és a csehsüvegboltozatot, majd a félhengerek áthatásával a kereszt- és kolostorboltozatot. De ezek csak az alapot adják az összetett boltozatok kialakításához.Szabálytalan terek lefedésével és különböző szélességű folyosókat lefedő dongaboltozatok összemetsződésével találkozhatunk.

A félgömbből síkmetszéssel nyert boltozatok:

Cseh boltozat	Cseh süvegboltozat	Csegelyes kupola

Hengerből áthatással nyert boltozatok:

Keresztboltozat	Kolostorboltozat

Szükségesek:

• Diasor
  
• Munkafüzet2025, 66. oldalától a végéig

Szemléltető videók:

További segédanyag: 

• Hallgatói munkák
• A GeomTech3D projekt keretében készült segédanyag (a szöveg horvát nyelvű, de az ábrák szemléletesek.) 
• A dongaboltozatok áthatásával keletkező boltozat szerkesztésének lépései táblaképek alapján
• Hasznos lista a forgásfelületek témakörhöz
• Boltozat szemléltetése naranccsal 

Forgásfelületek áthatása

Letölthető anyagok:

• Diasor 11 és Diasor 12
• A vetített diasorban szereplő animált ábra: kúp és henger áthatása
  
• Munkafüzet2025 56-65. oldalai

Ez a témakör a korábbi síklapú testek áthatása témakör továbbgondolása, ugyanis legvégül minden forgásfelület (de a szépen hullámzó ún. szabad formájú felületek is) poliéderekkel vannak közelítve a megjelenítések vagy az előállítások során. Ahhoz, hogy kezelhetők legyenek, bizonyos metszeteket kell ismernünk.
Az áthatásszerkesztés módszerei és ötletei attól függhetnek, hogy a felületek tengelyei egymáshoz képest hogyan helyezkednek el.

1. Egybeeső tengelyek

esetén a felületek  paralel körökben metszik egymást. A meridiángörbék közös pontjait kell keresni, ezek forgatásával nyerjük az áthatást adó kört (köröket).(Lásd Mf. 56. oldala)

2. Párhuzamos tengelyek 

esetén megadott felületeket a tengelyükre merőlegesen szeleteljük. Egy ilyen szeletelősíkban mindkét felület egy-egy (ritkán több) paralel köre rajzolódik ki. Ezek közös pontjai az áthatási görbe pontjai lesznek. Célszerű elég sűrűn szeletelni, hogy a kapott pontok minél jobban megmutassák az áthatási görbe formáját. (Lásd 57-61. oldalak)
Az áthatási görbének vannak szélső helyzetű (legmagasabban, legalacsonyabban lévő), kontúron lévő és a felületek közös szimmetriasíkjában lévő pontjai, ezeket jól választott szeletelősíkokkal tudjuk meghatározni. Ilyen helyzetet szemléltet az alábbi videó, amely 59. oldal feladatának a modelljén mutatja be a szeletelő eljárást.

A 60. oldal feladatának különlegessége, hogy a gömb érinti a kúpot. Ez azért érdekes helyzet, mert ebben a pontban kialakul egy ún. kettőspont. A görbén végighaladva ezen a ponton irányváltás nélkül jutunk át. A görbe futásának érzékeléséhez érdemes a 61. oldalon az áthatási vonalon 10-15 pontot beazonosítani és azokat az eredeti felületekkel együtt transzformálni.
A bal oldali ábra a modellt, a jobb oldalin a felületek kikapcsolva, csak a kontúrok, perem, és az áthatási görbe látszik:

3. Metsző helyzetű tengelyek

esetében olyan példákat fogunk látni, ahol a tengelyek merőlegesek egymásra. Miért jó ez? Ez egy igen fontos könnyítés egy álló forgásfelület és egy fekvő helyzetű henger esetén, mert így hengert vízszintes síkokkal könnyen tudjuk alkotókban metszeni.
A módszerünk:

SZELETELÉS !!!

Már nem azon kell gondolkodnunk, hogy mi a szeletelés, hanem alkalmazni azt SOKSZOR. Ezzel lehet biztosítani, hogy nagyon közel lesznek megszerkesztett pontok, amiket össze kell kötni. De látatlanban nem lehet megtanulni azt, hogy milyen is lesz egy áthatási vonal futása, ezért lássunk néhány példát:

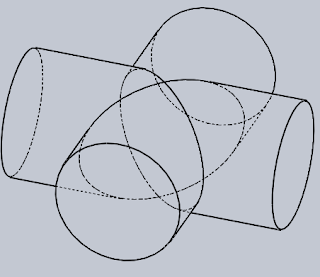
Ez a két henger egyenlő sugarú és a tengelyeik metsző helyzetben vannak. Alapban bárhogy elhelyezkedhetnek a térben, ezeken a képeken "fekvő" helyzetben vannak. Vagyis így, ahogy vannak, le lehet tenni őket az asztalra és egy lappal le lehet fedni őket. A geometria nyelvén ez azt jelenti, hogy alulról és felülről ugyanaz a síkpár érinti mindkét hengert → a legalsó és a legfelső alkotók metszéspontjaiban  a hengerek érintik egymást, és az áthatási vonal szétesik két ellipszisre. Ezek vonala a fenti képeken nagyon szépen kirajzolódik. Az ellipszisek síkjai egymásra merőlegesek, felülről nézve X-et formáznak. Ezzel a helyezettel még fogunk találkozni a Boltozatok témánál.

Ha az előbbi helyzeten csak annyit változtatunk, hogy csökkentjük a sugarát, akkor a fentebb említett érintkezést alul is és felül is elrontjuk. Egyszerűen a sárga henger vastagabb, a szürke vékonyabb és csak amiatt marad meg a levegőben, mert átdugtuk a sárga hengeren.

Ilyenkor az áthatásvonala két különálló zárt vonalból áll. Ezek szimmetrikusan helyezkednek el és kb olyasmi tekeredésük van, mint a Pringles csipsz peremének.

A PEREMet kell figyelni, és nem a csipsz felületét! A lényeg, hajlása van felfelé és lefelé is.

Hogyan érdemes szeletelni?

Az előbbi esetekben a forgástengelyek síkja mindkét felületnek szimmetriasíkja. Egy ilyen szeletelő síkban a hengerekből egy-egy alkotópárt találunk, melyek összesen 4 metszéspontot határoznak meg.

Vagyis a teendő: minél többször felvenni ilyen szeletelő síkot és négyesével megszerkeszteni a pontokat. Gyors és egyszerű eljárás! A munkafüzet 62. oldalán a vastagabb henger álló helyzetben van és a vékonyabb vízszintesen fúrja át. Ez azt jelenti, hogy ott a szeletelősíkjaink függőleges helyzetűek leszek, egészen pontosan a K2-vel párhuzamosak.

Az előbbi hengereket szeletelhetjük az egyik tengelyre merőlegesen is. Ekkor az egyik hengerből paralel kört, a másikból alkotópárt metszünk. Az egy szeletelősíkban lévő metszetek közös pontjai kijelölhetők. Valahogy így: 

Ez is gyors módszer, mint ahogy a képen is látszik, egy lépésben 4 pontot tudunk előállítani.

4. Kitérő helyzetű tengelyek

Ha a tengelyeket a metsző helyzetből elmozdítjuk, akkor kitérő tengelyeket kapunk. Kitérő tengelyek esetén általában az egyik tengelyre merőlegesen érdemes szeletelni. Ebben a szemléltető példában egy fekvő henger és függőleges tengelyű kúp került áthatásra. A szerkesztést megkönnyíti, ha a hengert vetítő helyzetűvé transzformáljuk. És ebben a helyzetben a szeletelést vízszintes síkokkal érdemes elvégezni, mert akkor a kúpból kimetszett kört két hengeralkotóval kell összemetszeni.

A 65. oldal feladatában a henger a K2 képsíkra merőleges, így nem kell transzformálni.

További segédanyag:

• Részlet Pethes Endre: 222 ábrázoló geometria feladat c. könyvéből. (XI. fejezet)
• gyakorló feladatok
• Illetve a jobb oldalon ajánlott irodalomból az Ábrázoló geometria szemléletesen című könyv megfelelő fejezete
• hallgatói munkák
• Hasznos lista a forgásfelületek témakörhöz
• A blog vendégposztjai közül:  Hengerek áthatása és Kúpok és hengerek áthatása

Gömb és tórusz metszése síkkal

 Letölthető anyagok:

• Diasor a gömb metszéséről + Diasor a tórusz metszéséről
• Munkafüzet2025 51. és 55. oldalai

Emlékeztető a gömb metszetei kapcsán:

• A gömb minden metszete kör, melyet a vetületeken körnek, ellipszisnek vagy átmérő hosszúságú szakasznak látunk. 
• A gömb metszetei egyre kisebbek, ahogy a középponttól távolodunk (Lásd itt). Ezt jól lehet szemléltetni azokkal a papírmodellekkel, melyek megfelelő sugarú körlapokból építhetők.
• Ha függőleges síkokkal felszeletelünk egy gömböt, akkor a metszetek nem csúszkálnak el, le, hanem egy adott magasságban maradnak.

 Gömb metszete általános helyzetben:

A legegyszerűbb olyan vetülettel (is) dolgozni, ahol a metsző sík vetítősík, vagyis egyetlen vonal jeleníti meg. Minden metszet esetén keressük a

• legmagasabban / legalacsonyabban fekvő pontokat (ha léteznek)
• a kontúrokon lévő pontokat
• a metszet (vagy a vetületének) nevezetes pontjait
• és annyi általános helyzetű pontot, hogy a metszet íve könnyen rajzolható legyen.

Egy kis kiegészítés ahhoz, hogy hogyan képzeljük el a gömb kontúrján lévő pontokat. A kontúr vonala mindig egy adott képsíkhoz (és így egy vetülethez) tartozik. A lenti forgatható ábrán a gömbön megjelenítettem a K2 képsíkkal párhuzamos főkört, melyet a képsíkra vetítve a gömb kontúrját kapjuk. Jól látszik, hogy ez a gömbi kör és metsző sík keresztezi egymást, mert a keletkező síkmetszet nem csak az elől lévő félgömbön keletkezik, hanem átnyúlik a hátsó félgömbre is. (Ezek a pontok narancsszínű megjelenítést kaptak a diasorban.)

 Tórusz metszetei :

A tórusz metszetei negyedrendű görbék, amely azt jelenti, hogy előfordulhat, hogy egy egyenesnek a metszettel 4 közös pontja van. Ahogy azt már korábban láttuk, a forgástengelyre merőleges metszésekkel a legtöbb esetben koncentrikus köröket kapunk, kivéve, amikor a tóruszt alulról vagy felülről érinti a sík. Ez az érintkezés azért "trükkös", mert matematikailag a legfelső kör ilyenkor duplán számítható ki, vagyis két koncentrikus kör, melyeknek egyenlő a sugara. Ugyanez érvényes az alsó körre is.  (http://fluid.itcmp.pwr.wroc.pl/~eichler/torus-przek2/img/tor-prze2.gif)

Ha a forgástengellyel párhuzamosan szeletelünk, akkor sokkal változatosabb metszeteket kapunk:  "ovális", "piskóta", nyolcas, "két szembefordított tojás" vagy két kör is lehet. A 8-as forma akkor jön létre, amikor a gyűrű belsejét megérinti a sík.

Ezeket a forgástengellyel párhuzamos metszeteket is használhatjuk sliceform modellek készítésére. (lásd lentebb)

Érdekesség, hogy tóruszból nemcsak a forgástengelyre merőleges  metszéssel kaphatunk kör metszeteket. Az alábbi ábra körei az ún.  Villarceau-körök, melyeket Yvon Villarceau (1813-1883) francia csillagászról és matematikusról neveztek el. A múlt század elején igazolták, hogy ezek a körök ugyanakkora szögben metszik a a tórusz összes paralel körét. A metsző síknak két helyen érintenie kell a tórusz belső oldalát, a jobb oldali ábra vetítősíkként mutatja ezt a helyzetet.

A képek forrása:

• http://fluid.itcmp.pwr.wroc.pl/~eichler/torus-przek2/img/torus-przek-2.gif
• http://upload.wikimedia.org/wikipedia/commons/f/f1/Villarceau_circles.gif
• http://momath.org/wp-content/uploads/bagel-circles-3.jpg

További segédanyag:

•  Gömbmetszetek sora (órán szerepelt)
  
• Táblaképek egy szerkesztésről (2016): Tórusz metszése síkkal
• Hallgatói munkák (több szkennelt ábra, tórusz metszése különböző állású síkokkal)
• Hasznos lista a forgásfelületek témakörhöz
• Gömb-modell készítése: https://papercraftetc.blogspot.com/2015/03/super-pi-day-ball.html
• Tórusz-modell készítése: https://papercraftetc.blogspot.com/2013/07/sliceforms-are-my-new-obsession.html
  

Kúp és henger metszése síkkal

Letölthető anyagok:

• Diasor pdf-ben
• Munkafüzet2025  52-54. oldalak
• Egy kúp metszése lépésenként: alkotókkal és paralelkörökkel. (Érdemes letölteni és úgy léptetni az oldalakat pdf megjelenítőben vagy böngészőben.)
  

Módszereinkben felhasználjuk a korábbi ismereteket:

•  Pont ábrázolása a kúp felületén: Ha a felületre alkotót illesztünk, akkor azt mindig az alapkör és a csúcspont közé kell rajzolnunk. Egy adott alkotón pont felvétele rendező egyenessel történik.
• Pont ábrázolása a kúp felületén: Ha a paralelkört illesztünk a felületre, akkor azt a forgástengely irányából (felülről) nézve valódi méretű körnek látjuk, míg szemből nézve egy átmérő hosszúságú szakasznak. Az így ábrázolt körvonalon rendezővel jelölhető pont. Az említett paralelkörök felülnézetben koncentrikus köröknek látszanak, de tudjuk, hogy különböző magasságokban vannak.
• Pont ábrázolása a henger felületén: Célszerű alkotókat választani, és azon adott magasságban választani a pontot. A hengeralkotók felülnézetben egyetlen pontnak látszanak.
• Transzformáció: annak érdekében, a metsző sík és a felület helyzetét jobban lássuk, célszerű olyan transzformációt alkalmazni, melyben a sík vetítősíkká válik. A módszer ismerős, a  síklapú testek metszésénél hasonló transzformációt alkalmaztunk.

Szeletelő módszer: a lényege, hogy egy forgásfelületet a tengelyére merőleges síkkal  metszve paralelkört (vagy köröket) kapunk, míg a felületet metsző síkot metszve egyenest. Minden ilyen szeletelő síkban a kimetszett alakzatok közös pontjai kijelölhetők. Ezzel a technikával a metszet nagyon sok pontja előállítható, melyeket görbe vonallal köthetjük össze.

Transzformációs módszer: a metsző síkot vetítősíkká transzformáljuk, és ezt a transzformációt a felületre is alkalmazzuk. A metsző sík jelöli ki a transzformáció irányát!  Ebben a speciális oldalnézetben könnyen kijelölhetők a metszet legmagasabban/legalacsonyabban lévő pontjai, de természetesen általánosabb helyzetű pontok is könnyen szerkeszthetők (különösen a henger és a kúp esetén).

Milyen pontokat keresünk?

• legmagasabban / legalacsonyabban fekvő pontokat (ha léteznek)
• a kontúrokon lévő pontokat
• a metszet (vagy a vetületének) nevezetes pontjait
• és annyi általános helyzetű pontot, hogy a metszet íve könnyen rajzolható legyen.

A szerkesztést könnyítheti, hogy a kúp is és a henger is egyenesekből álló felület. Egy-egy tetszőlegesen kiválasztott alkotóval az adott síkot metszve a keletkező görbe egy-egy pontját kapjuk.

Kúp metszete:

Ha olyan síkot veszünk, amely nem halad át a kúp csúcspontján, akkor az alábbi kép elég jól összefoglalja a lehetőségeket:

Forrás: Wikipédia

A fenti képen a metsző sík vetítősíknak látszik, és így maga a metszet is egy vonalként jelenik meg. Ha ez nem áll rendelkezésre, akkor transzformációval érdemes előállítani hasonló helyzetet. A lehetséges metszetek a következők:

• KÖR → a forgástengelyre merőleges síkkal
• ELLIPSZIS → minden alkotót metsző, de a tengelyre nem merőleges síkkal
• PARABOLA → egy alkotóval párhuzamos síkkal
• HIPERBOLA → két alkotóval párhuzamos síkkal

Természetesen, ha a metsző sík áthalad a kúp csúcspontján (és metszi is a palástot), akkor alkotópárt kapunk. Illetve a kúpot az alkotók hosszabbításával könnyen lehet ún. kettős kúppá alakítani. Ezt azért érdemes elképzelni, mert csak ekkor jön létre a hiperbolametszet mindkét ága. A metszetek változásait jól szemlélteti az alábbi animált ábra:

 Az előbbi ábra bizonyos pillanataiban lehet látni,hogy a metszet lehet alkotópár abban az esetben, a sík áthalad a kúp csúcspontján. Ezt érdemes külön megemlíteni:

Ilyen egymás mögötti alkotókat akkor láttunk, amikor a kúp felületén pontokat ábrázoltunk.
Az alkotók segítségével kerül egy síkmetszet megszerkesztésre az alábbi videóban:

Henger metszete:

Forrás: http://ludens.elte.hu/~vima/

A henger esetén jóval kevesebb lehetőségünk van: ferde helyzetű síkkal metszve mindig ellipszist kapunk. Az ellipszis vetülete az 1. képen kör, míg a 2. képen ellipszis lesz. Ebben a videóban jól látszik, hogy ha a sík állása egyre jobban eltér a vízszintestől, akkor az ellipszis metszet alakja elkezd nyúlni. Illetve az ellipszis egy része létre sem jön, ha pl. a sík a henger fedőkörébe is bele tud metszeni.

Tapasztalatgyűjtéshez érdemes belenézni az alábbi videóba:

További segédanyagok:

• Gyakorlat 2020-ból
• Hasznos lista a forgásfelületek témakörhöz
  

Forgásfelületek keletkezése és metszésük egyenessel

A forgásfelületek elnevezés egy összefoglaló név minden olyan felületre, amely egy görbe egy adott tengely körüli megforgatásával keletkezik. A forgatás az egyik gyakran alkalmazott módszer különböző formák alakjának modellezésére, a szoftverek többnyire Rotate, Revolution, Revolved Boss/Base parancsokat használnak a generálásukra.

Felületek előállítását szemléltető eszköz a MoMath matematikai múzeumban.

Ha a megforgatandó görbe alakját figyeljük, akkor az többnyire egy hullámzó vonal lehet, ha pl. egy váza formáját keressük. De mérnöki alkalmazásokban alapelemként olyan felületeket használnak, melyek egyenes vagy kör megforgatásával keletkeznek. 

Letölthető anyagok:

• Diasor 
• Munkafüzet2025 45.-50. oldala
• A diasor animált ábrái elérhetők ITT  

A henger és a kúp vonalfelületek, ami azt jelenti, hogy a felület minden pontján áthalad egy egyenes, vagy annak egy szakasza. Az ábrázolásoknál kerüljük a végtelenbe futó felületdarabokat, ezért mindig adott magasságú hengerrel és kúppal fogunk találkozni. Jellemzőjük, hogy síkba fejthetők, azaz síklapra szerkesztett hálójuk alapján papírmodelljeik előkészítők.

 A henger és a kúp  esetén közös tulajdonság az, hogy a felületi pontok keresése kétféle módszerrel valósítható meg: paralelkörrel vagy alkotóval. Az alkotó megjelenítése ahhoz hasonló, amikor a hasáb/gúla oldalélét rajzoltuk meg. És ez nem véletlen, hiszen ha növeljük a hasáb/gúla oldaléleinek és ezzel az oldallapjainak a számát, akkor az oldalfelület elkezd kisimulni, és végül hengert/kúpot kapunk.

A paralelkör megjelenése ahhoz hasonló, amikor a hasábokat/gúlákat egy adott magasságban elmetszettük egy vízszintes síkkal. A henger esetén mindig azonos méretű metszeteket kapunk, míg a kúp esetén a csúcs felé haladva egyre kisebbeket. Ezek a modern mászókák elég jól szemléltetik ezt a tényt.

Nagyon fontos, hogy minden felületi ponton át egy alkotó és egy paralelkör vehető fel!


A gömb és a tórusz kör megforgatásával keletkezik, a gömb esetén a forgástengely áthalad a kör középpontján, míg a tórusz esetében nem. A felületi pontok megadásakor a meridiánmetszet nem igazán használható, mivel ezek többnyire ellipszisként látszanának. Így csak a forgástengelyre merőleges metszetek, azaz a paralelkörök használhatók.
A tórusz esetén többnyire a lyukas "változatát" ábrázoljuk, amely hasonlít az úszógumi, biciklibelső formájához, vagy éppen az amerikai fánk alakjához.

A  tórusz felületére való pontillesztést az 1. képről indítva is szerkeszthetjük.  A lépéseket bemutató videó elérhető itt..

Továbbá fontos, hogy emlékezzünk arra, hogy a gömb bármely síkmetszete kör, csaknem minden esetben fog körnek látszani. Ha a metsző sík egyik képsíkkal sem párhuzamos, akkor a metszet vetülete ellipszis lesz.
Ha már a modern mászókákat hívtam segítségül, akkor megmutatom,hogy milyen volt a gyermekkorom játszótere. Ilyen gömbmászókán lógtunk, ha a rakétát a fiúk elfoglalták:

A hosszanti cikkek (olyanok,mint a narancsgerezdek) határai éppen a meridiánmetszetek, és néhány magasságban megvannak a paralelkörök is. A mászóka fokai pedig egyenes szakaszokkal íveket helyettesítettek.
Hasonló ötlet 48. oldal feladatának megoldást szemlélteti. És mi is a lényeg? Ha egy gömböt egy egyenessel el akarunk metszeni, akkor az egyenesre bárhogy is illesztünk síkot, akkor a gömb metszete éppen a keresett szúráspontokban metszi az egyenest.

Csak nem mindegy, hogy hogyan vesszük fel a síkot! Ha függőleges síkkal metszünk, akkor a metszet könnyen leforgatható. Az alábbi animált ábra éppen a szerkesztést mutatja be: http://fluid.itcmp.pwr.wroc.pl/~eichler/kula-pr/img/anim-k-pr.gif 

Ebben az esetben kérdés:
Milyen magasan kell keresni a gömbből függőleges síkkal metszett  kör középpontját? Már az almás kép is mutatja, hogy a metszetek nem csúszkálnak el, le, hanem egy adott magasságban maradnak.

Hasznos segítség:

• Pethes Endre: 222 Ábrázoló geometriai feladat (IX. és X fejezet),melyeket elérthet ezen a  linken
  
• Gömb metszése vetítősíkkal + feladatlap
• Hasznos lista a forgásfelületek témakörhöz
• Gyakorlat (2021)

 

Gúlák és hasábok áthatása - amikor a hasáb nincs vetítő helyzetben

Felhasznált korábbi ismeretek:

• Transzformáció, mellyel elérhető, hogy egy hasáb élei (oldallapjai) az új képsíkra merőlegesek legyenek. Ebben az új nézetben eldönthető, hogy hány pont határozza meg az áthatási töröttvonalat.
  
• Vetítősík és egyenes döféspontjának szerkesztése. A metszéspont az egyik képen azonnal látható, a másik kép rendezővel szerkeszthető.
• Síkra illeszkedő egyenes: a sík körvonalát két pontban metszi, és ezt a rendezők is mutatják.
• Síkok metszésvonala. Két közös pont által megadva, speciális helyzetekben is.

Letölthető anyagok:

• Diasor pdf-ben (67. oldaltól)
  
• Munkafüzet2025  38-39. oldala

Bevezetésként nézzünk egy nem túl bonyolult példát! Az alábbi ábrán egyik test sincs vetítő helyzetben:

(Forrás:bme.hu)

És látjuk a megoldást is: a vetítő helyzetet egyetlen transzformációval lehet elérni, amelyben a fekvő helyzetű hasáb oldalélei vetítőegyenesekké válnak. A transzformációt CSAK ez a hasáb fogja meghatározni, az x14 tengely merőleges a hasáb oldaléleinek első képére. Ezt követi a transzformáció végrehajtása, és ekkor kapjuk meg azt a kedvezőbb vetületet, amelyben látszik, hogy összesen hány pontot kell  megszerkesztenünk. Az I. és IV. kép felhasználásával az áthatás minden pontja megszerkeszthető, a II. képet a transzformáció visszafelé történő alkalmazásával szerkesztjük.

A feladatunk első lépése is a transzformáció lesz.

Magát a transzformációs lépéseket nem részletezném, mert már megtanultuk. A végeredmény azt mutatja, hogy a hasáb egyetlen háromszögként jelenik meg, amely körül látjuk a gúla vetületét.

Most lehet átnézni a teendőket:

• A hasáb mindhárom oldaléle (mint pontoknak látszó egyenesek) a gúla kontúrján belül van ---> élenként 2-2 metszéspontot kell szerkeszteni.
• A gúla MA és MB élei elkerülik a hasábot,csak az MC él metsz bele ---> 2 metszéspontot kell szerkeszteni. (Erre még később kitérünk, mert itt különlegesebb helyzet állt elő!)
• Tehát 6 + 2 pontot kell szerkeszteni az 1.képre is és a 2. képre is a IV. képből kiindulva.
• Összekötés: a szabály alapján az 1. képen is és a 2. képen is összekötjük a pontokat. 
• Láthatóság szerinti kihúzás

A lépésekhez a diasor lépéseit kell követni, néhány pillanatképek most ki is emelek:

• Metszés az MC egyenessel. Az 1. és IV. kép vonatkozásában ez az él nagyon meredeken fut, majdnem merőleges a az x14 tengelyre. Ebben az esetben nem tanácsos a rendezőket használni, hogy az1' és 2' pontokat megkeressük! Figyeljék csak a zöld rendező vonalakat! Nagyon közel futnak egymáshoz és nagyon kis szögben fogják metszeni az M'C' élt. Szinte biztos, hogy kézi szerkesztéssel elmozdulnak a pontok arról a helyről, ahol lenniük kellene. Ezt csak akkor lehetne észrevenni, amikor a 2. képeket is meghatároznánk, és a pontok nem lennének benne a hasábban.

• Inkább így oldjuk meg:

 

És végül a 2.képről rendezőket indítva jelöljük ki az 1' és 2' pontokat.

• A szerkesztés folytatására a következőket ajánlom:

 

• Fontos, hogy a fenti kezdésekkel a 3' és 4' pontok kétszer is meghatározásra kerülnek, DE NEM LESZ BELŐLÜK 2 DB! A b egyenesnek csak két közös pontja lehet a gúlával. Ha pontosan dolgoznak, akkor a két háromszög formájú metszet a 3' és 4' pontokban metszi egymást.

Gyakorló feladat:

• Egy feladat (Gyakorló feladatok / Hasábok és gúlák áthatása / 8. oldal) megoldása, ahol a hasáb vízszintes éleivel való metszéseket vízszintes vágásokkal szerkesztették és nem azzal a módszerrel, hogy a hasáb lapot hosszabbítottuk meg. A megoldás után a test lapjait különböző színekkel jelölték, ami segít abban, hogy melyik lapot láthatjuk.A kék, barna, piros lapok mindkét képen látszanak, a sárga és a zöld pedig hátrafelé fordulnak, így nem láthatók szemből.
  
• Ugyanennek a feladatnak a megoldása táblaképeken, lépésekben: