2021. szeptember 27., hétfő

Metszési feladatok 1. (2021)

 Ezen a héten az illeszkedési feladatokra alapozva metszési feladatokat fogunk megoldani. 

A síkok esetén egyszerűbb helyzetekkel foglalkozunk, amikor mindkét sík vagy csak az egyikük van vetítő helyzetben. Ezeket a feladatokat elemezve fogunk eljutni az általánosabb helyzetek megoldásához.

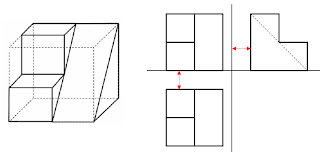
 A bal oldali ábrán mindkét sík függőleges helyzetű, és ebből a helyzetből következik, hogy a metszésvonaluk is függőleges helyzetű lesz. A jobb oldali ábrán a síkok is és így a metszésvonaluk is merőleges lesz a K2 képsíkra.

Általában azonban nem vagyunk ennyire szerencsések, mert nem mondható meg a metszésvonal állása. A szerkesztés ekkor azon alapszik, hogy egy egyenes és egy síklap metszéspontját meg tudjuk-e határozni.

Általános helyzetű térelemek esetében a fedő egyenespár módszerét alkalmazhatjuk. Ennek az lesz a lényege, hogy az elképzeljük az egyenes egyik vetítősíkját, és azzal az adott síkba metszünk. Ekkor egy olyan egyenest kapunk, amely az adott egyenes alatt/fölött halad, és közben át is metszi azt.
Ez ábrán a V1 első vetítősíkot választottam, amely az m egyenesben metszi a háromszöglap síkját. Az első képen (felülnézetben) az adott egyenes és az m egyenes ugyanabban  a vonalban látszik, míg a 2. képen (szemből nézetben) azt látjuk, hogy hogy az e és m egyenesek metszőek. Ezt a metsző helyzetet természetesen bármely oldalnézet is megmutatná.
A lenti interaktív ábrán az előbbi gondolatokat tudja ellenőrizni a modell forgatásával. A bal egérgomb lenyomása mellett mozgatva az egeret a modell forgatható, a görgővel a nézőpont közelíthető/távolítható.

 




Láthatóság:

Minden metszési feladatot szemléletessé fogunk tenni az ún. láthatóság szerinti kihúzással. Az adott síkot síklapként képzeljük. A feladatunk az, kiválasztjuk a takarásban lévő szakaszokat és területeket és szaggatott vonallal jelöljük azokat. A látható szakaszokat folyamatos vonallal jelöljük, általában vastagabb vonallal, vagy ahogy a diákon is látható színes vonallal. Az eljárás végén egy szemléletes képet kapunk az alakzatok átmetsződéséről.

Letölthető anyagok:

További segédanyag

  • Sulinet tudásbázis (link)
     
Bejegyezte: dátum: Nincsenek megjegyzések:
Címkék: , , , , ,

2021. szeptember 11., szombat

Illeszkedési feladatok (2021)

A térelemek ábrázolása során gyakran előfordul az, hogy illeszkedő térelemeket kell ábrázolnunk. Az illeszkedésnek vannak látható feltételei, melyekre ezen a héten több figyelmet fogunk szánni. A főbb tudnivalók vázlatosan:

  • Pont és egyenes illeszkedése:
    Jusson eszünkbe, hogy ha egy drótszálra gyöngyöt fűzünk, akkor  bárhonnan is nézzük, mindig azt látjuk, hogy a gyöngy a szálon van.
    Ábrázoláskor fontos, hogy mindkét képen látható legyen az "illeszkedik" helyzet, vagyis a pont első képe az egyenes első képére, a pont második képe az egyenes második képére illeszkedjen, és természetesen a pont képeit rendezővel tudjuk összekötni.  
  • Egyenes és sík illeszkedése:
    A természetben a pókháló emlékeztet erre legjobban. A pók úgy tud a tartószálak által feszített felületen (ez gyakran síknak vehető) maradni, ha a fő szálak közé újabb szálakat sző. Ezek a szálak gyakran megereszkednek, de az elvet jól szemléltetik.
    Ábrázoláskor egy egyenes síkra való illesztése már bonyolultabb, ugyanis az már ismert elemekhez kell "ragasztanunk" az újabbat. A síkot úgy kell tekinteni, mintha egy átlátszó fólia lenne, amelyre rajzolhatunk. Metsző egyenes párral adtunk meg egy síkra minden újabb egyenes az adott egyenesekkel alkotott metszéspontjai által rögzíthető! Adott egyenesek egyikével párhuzamos egyenes pedig a másikkal alkotott metszéspont és a párhuzamosság által illeszthető.
  • Pont és sík illesztése:
    Ha az előbbi pókháló szálain kicsapódik a pára, akkor az előbbi két esetünk kombinálódik. A vízcsepp csak akkor tud a háló síkjában maradni, ha a szálakon van.
    A pont síkra történő illesztése viszont összetettebb. Az új pontot a sík régi adataihoz csak egy újabb egyenes segítségével tudjuk kötni. Vagyis először egy új egyenest illesztünk a síkra, majd azon jelöljük ki az új pontot.
Természetesen ezek általános elvek, a speciális helyzetű elemek esetében eleve egyszerűsödnek, más esetekben nekünk kell keresni az egyszerűsítés lehetőségét.

Letölthető anyagok:

További segédanyag

A bejegyzés képeinek forrása:

  •  http://meska.hu/img/blog/post_9ee0366ea5282d16251d4f9633d383a4639.jpg
  •  http://7-themes.com/data_images/out/24/6849391-spider-web.jpg
  •  http://farm3.static.flickr.com/2533/3838029983_094c7feece_o.jpg

 

Bejegyezte: dátum: Nincsenek megjegyzések:
Címkék: , , ,

2021. szeptember 8., szerda

Monge-rendszer, vetületek, modellek (2021)

Az 1.héten a térelemek ábrázolásával foglalkozunk. Megismerjük a Monge-rendszert, amelyben egyszerre kell dolgoznunk egy alakzat elöl- és felülnézetével. A vetületek helyzetéből kell majd következtetnünk az alakzatok térbeli helyzetére, a képsíkokhoz viszonyított helyzetükre.

  • Alapfogalmak: képsíkrendszer, rendező, térnegyedek, pontok ábrázolása a térnegyedekben, pont távolsága a képsíkoktól.
  • Síkok megadása különböző elemekkel (3 általános helyzetű ponttal, metsző egyenespárral, párhuzamos egyenespárral, pont és rá nem illeszkedő egyenessel), síkok helyzete a képsírendszerben, térbeli helyzet visszaállítása, modellezés.
Forrás: Sokszínű matematika 5. osztály
  • Meg kell említenünk, hogy mi az európai ábrázolási rendszert fogjuk használni. Az alakzatot egymásra merőleges képsíkok által határol „szobasarokba” helyezzük, majd a síkokra merőlegesen vetítjük. A vetítés után a képsíkokat kihajtogatjuk a vetületekkel együtt. A vetítések során fontos, hogy a sorrend minden esetben: szemlélő – alakzat – képsík.
    Általában következő vetületek készülnek: elölnézet, felülnézet, oldalnézet (balnézet).
    Szükség esetén kiegészíthető a rendszer a teljes „bedobozoláshoz” a hiányzó három síkkal, melyek a következő képek keletkeznek: alulnézet, hátulnézet, oldalnézet (jobbnézet).
  • Csonkolt kocka axonometrikus képének felhasználásával készítse el a vetületi ábrákat! (felülnézet, elölnézet, oldalnézet) A vetületei ábrákon a takart vonalakat is tüntesse fel vékony szaggatott vonallal.
 

Letölthető anyagok:


További segédanyag

Bejegyezte: dátum: Nincsenek megjegyzések:
Címkék: , , , , , , ,
Feliratkozás: Bejegyzések (Atom)